题目内容
AB是圆O的直径，EF切圆O于C，AD⊥EF于D，AD=2，AB=6，则AC长为（ ）
分析：在圆中线段利用由切割线定理证得∠ACD=∠ABC，进而利用直角三角形相似的判定得到三角形相似，得比例式求得AC即可．
解答：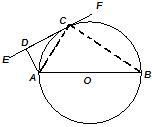
解：连接AC、BC，
则∠ACD=∠ABC，
又因为∠ADC=∠ACB=90°，
所以△ACD～△ACB，
所以
=
，即
=
解得AC=2
．
故选A．
解：连接AC、BC，则∠ACD=∠ABC，
又因为∠ADC=∠ACB=90°，
所以△ACD～△ACB，
所以
| AD |
| AC |
| AC |
| AB |
| 2 |
| AC |
| AC |
| 6 |
解得AC=2
| 3 |
故选A．
点评：此题考查的是圆的切线的性质定理的证明、直角三角形的性质及相似三角形的判定与性质定理，属于基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
3、如图，AB是圆O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F．
（2013•湖北）如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．
（2013•广东）（几何证明选讲选做题）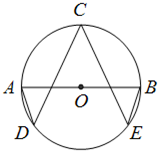
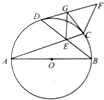如图，AB是圆O的直径，C，D是圆O上两点，AC与BD相交于点E，GC，GD是圆O的切线，点F在DG的延长线上，且DG=GF．求证：