题目内容
如图,AB是圆O的直径,点C,D,E都在圆O上,若∠C=∠D=∠E,则∠A+∠B=
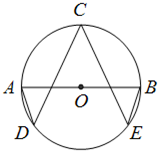
135°
135°
.
分析:由∠C=∠D=∠E,得弧AC=弧BC=弧DE,即弧AC与弧BC的和是半圆,则弧AC对的圆心角是90度,弧AC对的圆周角是45度,则弧AC与弧BC与弧DE分别所对的圆心角的和是270度,有弧AD与弧BE的和的度数是90度,即,弧AD与弧BE分别所对的圆周角的和为45度由圆周角定理可求.
解答:解:∵∠C=∠D=∠E,AB为圆O的直径
∴弧AC,弧BC,弧DE相等,且等于圆周的
∵弧AC与弧BC的和是半圆,
∴弧AC对的圆心角是90°,弧AC对的圆周角是45°,
∴弧AC与弧BC与弧DE分别所对的圆心角的和是270°,
∴弧AD与弧BE的和的度数是90°,
即,弧AD与弧BE分别所对的圆周角的和为45°,
∵A,B所对的弧分别为弧DB,弧AE,且两端弧长总和为圆周的
由圆周角定理可得,∠A+∠B=180×
=135°
故答案为:135°
∴弧AC,弧BC,弧DE相等,且等于圆周的
| 1 |
| 4 |
∵弧AC与弧BC的和是半圆,
∴弧AC对的圆心角是90°,弧AC对的圆周角是45°,
∴弧AC与弧BC与弧DE分别所对的圆心角的和是270°,
∴弧AD与弧BE的和的度数是90°,
即,弧AD与弧BE分别所对的圆周角的和为45°,
∵A,B所对的弧分别为弧DB,弧AE,且两端弧长总和为圆周的
| 3 |
| 4 |
由圆周角定理可得,∠A+∠B=180×
| 3 |
| 4 |
故答案为:135°
点评:本题利用了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目


 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.



 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数