题目内容
已知函f(x)=lnx-ax2+(2-a)x.
①讨论f(x)的单调性;
②设a>0,证明:当0<x<
时,f(
+x)>f(
-x);
③函数y=f(x)的图象与x轴相交于A、B两点,线段AB中点的横坐标为x0,证明f′(x0)<0.
①讨论f(x)的单调性;
②设a>0,证明:当0<x<
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
③函数y=f(x)的图象与x轴相交于A、B两点,线段AB中点的横坐标为x0,证明f′(x0)<0.
分析:①求出函数f(x)的定义域,然后在定义域内分a>0,a≤0两种情况解不等式f'(x)>0,f'(x)<0可得函数的单调区间;
②设函数g(x)=f(
+x)-f(
-x),只需证明g(x)>0即可,进而转化为利用导数求函数的最值;
③由①易判断a≤0时不满足条件,只需考虑a>0时情形,由①可得f(x)的最大值为f(
),且f(
)>0,设A(x1,0),B(x2,0),0<x1<x2,则0<x1<
<x2,由②可推得f(
-x1)>f(x1)=f(x2)=0,借助函数单调性可得结论;
②设函数g(x)=f(
| 1 |
| a |
| 1 |
| a |
③由①易判断a≤0时不满足条件,只需考虑a>0时情形,由①可得f(x)的最大值为f(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
解答:解:①函数f(x)的定义域为(0,+∞),
f'(x)=
-2ax+(2-a)=-
,
(i)当a>0时,则由f'(x)=0,得x=
,
当x∈(0,
)时,f'(x)>0,当x∈(
,+∞)时,f'(x)<0,
∴f(x)在(0,
)单调递增,在(
,+∞)上单调递减;
(ii)当a≤0时,f(x)>0恒成立,
∴f(x)在(0,+∞)单调递增;
②设函数g(x)=f(
+x)-f(
-x),
则g(x)=[ln(
+x)-a(
+x)2+(2-a)(
+x)]-[ln(
-x)-a(
-x)2+(2-a)(
-x)]=ln(1+ax)-ln(1-ax)-2ax,
g'(x)=
+
-2a=
,
当x∈(0,
)时,g'(x)>0,而g(0)=0,
∴g(x)>g(0)=0,
故当0<x<
时,f(
+x)>f(
-x);
③由①可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f(
),且f(
)>0,
不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1<
<x2,
由②得,f(
-x1)=f(
+
-x1)>f(x1)=f(x2)=0,
又f(x)在(
,+∞)上单调递减,
∴
-x1<x2,于是x0=
>
,
由①知,f'( x0)<0.
f'(x)=
| 1 |
| x |
| (2x+1)(ax-1) |
| x |
(i)当a>0时,则由f'(x)=0,得x=
| 1 |
| a |
当x∈(0,
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,
| 1 |
| a |
| 1 |
| a |
(ii)当a≤0时,f(x)>0恒成立,
∴f(x)在(0,+∞)单调递增;
②设函数g(x)=f(
| 1 |
| a |
| 1 |
| a |
则g(x)=[ln(
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
g'(x)=
| a |
| 1+ax |
| a |
| 1-ax |
| 2a3x2 |
| 1-a2x2 |
当x∈(0,
| 1 |
| a |
∴g(x)>g(0)=0,
故当0<x<
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
③由①可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,
故a>0,从而f(x)的最大值为f(
| 1 |
| a |
| 1 |
| a |
不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1<
| 1 |
| a |
由②得,f(
| 2 |
| a |
| 1 |
| a |
| 1 |
| a |
又f(x)在(
| 1 |
| a |
∴
| 2 |
| a |
| x1+x2 |
| 2 |
| 1 |
| a |
由①知,f'( x0)<0.
点评:本题考查利用导数研究函数的单调性、最值及不等式的证明问题,考查分类讨论思想,本题综合性较强,难度较大,对能力要求较高.

练习册系列答案
相关题目
 ax2+bx(a≠0).
ax2+bx(a≠0). ax2+bx(a≠0).
ax2+bx(a≠0).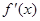 为f(x)的导函数,求证:
为f(x)的导函数,求证:
