题目内容
7. 春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.
春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.(1)问该学生监控抽查采取的是什么抽样方法?中位数落在那段区间内?
(2)估计这40辆小型汽车的平均车速;
(3)若从该学生抽查的受到罚款的车辆中随机抽取2辆车的罚款作为该学生的学业赞助费,求该学生所得学业赞助费超过200元的概率.
分析 (1)根据抽样方法的特征,判断是系统抽样,根据频率分布直方图,求出样本数据的众数和中位数的估计值求出中位数落在的区间;
(2)直接利用平均数就是公式求解即可.
(3)受到罚款的车辆共6辆,从6辆小型汽车中任取2辆共有15种取法,然后求解该学生所得学业赞助费超过200元的概率.
解答 解:(1)监控抽查采取的是系统抽样方法…(1分)
∵频率分布直方图中a=0.1-(0.005+0.01×3+0.025)=0.04
∴6段区间的人数依次是4,10,16,4,4,2人
故中位数落在(90,100]内…(3分)
(2)这40辆小型汽车的平均车速为4×75+10×85+16×95+4×105+4×115+2×12540=954×75+10×85+16×95+4×105+4×115+2×12540=95(km/h)…(6分)
(3)受到罚款的车辆共6辆,从6辆小型汽车中任取2辆共有15种取法…(8分)
罚款总金额超过200元的情形有9种…(10分)
故该学生所得学业赞助费超过200元的概率为P=915=35P=915=35…(12分)
点评 本题考查均值的求法,考查离频率分布直方图的应用,古典概型概率的求法,解题时要认真审题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则此几何体不可能是( )


| A. |  | B. |  | C. |  | D. |  |
15.已知集合A={x|y=√x2−2x−3√x2−2x−3},B={y|y=3sinx-1},则集合B∩∁RA=( )
| A. | (-1,2] | B. | ∅ | C. | [-4,-1] | D. | [-4,3) |
12.在极坐标系中,曲线ρ=2cosθ是( )
| A. | 过极点的直线 | B. | 半径为2 的圆 | ||
| C. | 关于极点对称的图形 | D. | 关于极轴对称的图形 |
16.若不等式(-2)na-3n-1-(-2)n<0对任意正整数n恒成立,则实数a的取值范围是( )
| A. | (1,43) | B. | (12,43) | C. | (1,74) | D. | (12,74) |
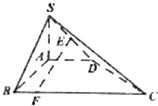 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=