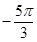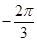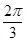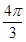题目内容
已知函数 .
.
(Ⅰ) 求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ) 已知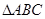 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.
 .
.(Ⅰ) 求函数
 的最小值和最小正周期;
的最小值和最小正周期;(Ⅱ) 已知
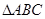 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.(Ⅰ)  的最小值为
的最小值为 ,最小正周期为
,最小正周期为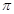 (Ⅱ)
(Ⅱ) 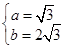
 的最小值为
的最小值为 ,最小正周期为
,最小正周期为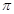 (Ⅱ)
(Ⅱ) 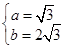
本题主要考查三角函数的恒等变换,正弦函数的周期性、定义域和值域,两个向量共线的性质,正弦定理、余弦定理的应用,属于中档题.
(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为 sin(2x-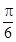 )-1,由此求出最小值和周期.(Ⅱ)由f(C)=0可得sin(2C-
)-1,由此求出最小值和周期.(Ⅱ)由f(C)=0可得sin(2C- 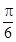 )=1,再根据C的范围求出角C的值,根据两个向量共线的性质可得 sinB-2sinA=0,再由正弦定理可得 b=2a.再由余弦定理得9=a2 +b2-2abcos
)=1,再根据C的范围求出角C的值,根据两个向量共线的性质可得 sinB-2sinA=0,再由正弦定理可得 b=2a.再由余弦定理得9=a2 +b2-2abcos 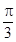 ,求出a,b的值.
,求出a,b的值.
解:(Ⅰ)
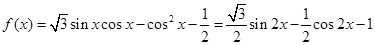
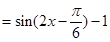
∴ 的最小值为
的最小值为 ,最小正周期为
,最小正周期为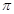 .
.
(Ⅱ)∵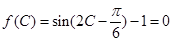 , 即
, 即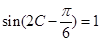
∵ ,
,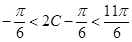 ,∴
,∴ 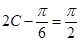 ,∴
,∴ 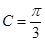 .
.
∵ 共线,∴
共线,∴ 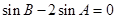 .
.
由正弦定理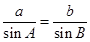 , 得
, 得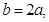
∵ ,由余弦定理,得
,由余弦定理,得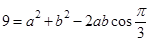 ,
,
解方程组①②,得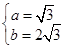 .
.
(Ⅰ)利用三角函数的恒等变换化简函数f(x)的解析式为 sin(2x-
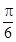 )-1,由此求出最小值和周期.(Ⅱ)由f(C)=0可得sin(2C-
)-1,由此求出最小值和周期.(Ⅱ)由f(C)=0可得sin(2C- 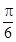 )=1,再根据C的范围求出角C的值,根据两个向量共线的性质可得 sinB-2sinA=0,再由正弦定理可得 b=2a.再由余弦定理得9=a2 +b2-2abcos
)=1,再根据C的范围求出角C的值,根据两个向量共线的性质可得 sinB-2sinA=0,再由正弦定理可得 b=2a.再由余弦定理得9=a2 +b2-2abcos 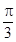 ,求出a,b的值.
,求出a,b的值.解:(Ⅰ)

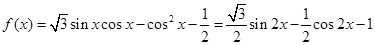
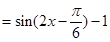
∴
 的最小值为
的最小值为 ,最小正周期为
,最小正周期为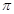 .
. (Ⅱ)∵
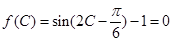 , 即
, 即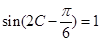
∵
 ,
,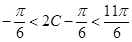 ,∴
,∴ 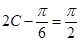 ,∴
,∴ 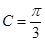 .
. ∵
 共线,∴
共线,∴ 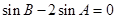 .
.由正弦定理
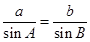 , 得
, 得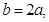
∵
 ,由余弦定理,得
,由余弦定理,得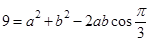 ,
, 解方程组①②,得
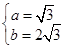 .
. 
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 的图像沿着直线
的图像沿着直线 的方向向右上方平移两个单位,得到
的方向向右上方平移两个单位,得到 ,则
,则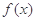 的解析式为( )
的解析式为( )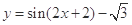
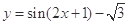
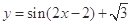
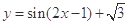
 .
.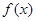 的最小正周期;(2)求
的最小正周期;(2)求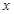 的集合.
的集合.  的图象,只要将
的图象,只要将 的图象( )
的图象( )
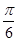
 ,
, .
. 的最小正周期;(2)求
的最小正周期;(2)求 ,求
,求 的值.
的值.  的最大值与最小值之和为( )
的最大值与最小值之和为( )
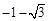
 的图象与函数
的图象与函数 的图象在开区间
的图象在开区间 上的一种较准确的判断是
上的一种较准确的判断是 )(ω>0,|
)(ω>0,| ,x∈R)的部分图象如图所示,则该函数为( )
,x∈R)的部分图象如图所示,则该函数为( )
 x+
x+ )
) 恒成立,其中
恒成立,其中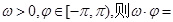 ( )
( )