题目内容
设函数 .
.
(1)求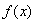 的单调区间;
的单调区间;
(2)设函数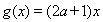 ,若当
,若当 时,
时, 恒成立,求
恒成立,求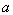 的取值范围.
的取值范围.
【答案】
(1) 当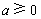 时,
时,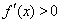 ,所以
,所以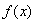 在
在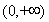 上是增函数当
上是增函数当 时,
时,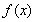 在
在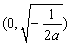 上是增函数,在
上是增函数,在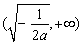 上是减函数;(2)
上是减函数;(2) 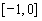
【解析】
试题分析:(1)根据导数公式求出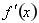 ,对于含有的参数
,对于含有的参数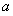 要进行讨论,
要进行讨论,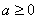 或
或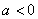 两种情况;(2)设
两种情况;(2)设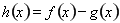 ,将
,将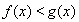 恒成立,转化成
恒成立,转化成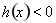 恒成立,所以求
恒成立,所以求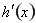 ,将
,将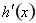 分解因式,讨论
分解因式,讨论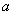 的范围,确定
的范围,确定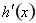 的正负,讨论
的正负,讨论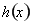 的单调性,确定
的单调性,确定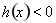 恒成立的条件,确定
恒成立的条件,确定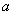 的范围,此题考察了导数的应用,属于中等偏上的系统,两问都考察到了分类讨论
的范围,此题考察了导数的应用,属于中等偏上的系统,两问都考察到了分类讨论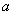 的范围,这是我们在做题时考虑问题不全面,容易丢分的环节.
的范围,这是我们在做题时考虑问题不全面,容易丢分的环节.
试题解析:(1)解:因为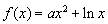 ,其中
,其中 . 所以
. 所以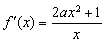 , 2分
, 2分
当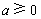 时,
时,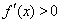 ,所以
,所以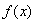 在
在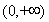 上是增函数 4分
上是增函数 4分
当 时,令
时,令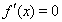 ,得
,得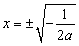
所以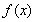 在
在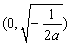 上是增函数,在
上是增函数,在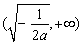 上是减函数. 6分
上是减函数. 6分
(2)解:令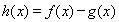 ,则
,则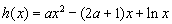 ,
,
根据题意,当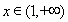 时,
时,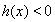 恒成立. 8分
恒成立. 8分
所以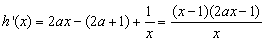
(1)当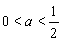 时,
时,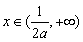 时,
时,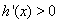 恒成立.
恒成立.
所以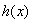 在
在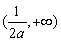 上是增函数,且
上是增函数,且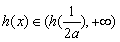 ,所以不符题意 10分
,所以不符题意 10分
(2)当 时,
时,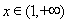 时,
时,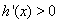 恒成立.
恒成立.
所以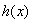 在
在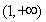 上是增函数,且
上是增函数,且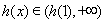 ,所以不符题意 12分
,所以不符题意 12分
(3)当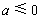 时,
时,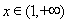 时,恒有
时,恒有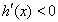 ,故
,故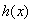 在
在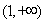 上是减函数,
上是减函数,
于是“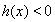 对任意
对任意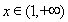 都成立”的充要条件是
都成立”的充要条件是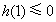 ,
,
即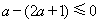 ,解得
,解得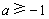 ,故
,故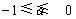 .
.
综上所述,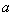 的取值范围是
的取值范围是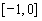 . 15分
. 15分
考点:1.利用导数求函数的单调区间;2.利用导数解决恒成立的问题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 。
。 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;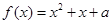 在区间[0, 2] 恰有两个不等实根,求a的取值范围。
在区间[0, 2] 恰有两个不等实根,求a的取值范围。 ,(1)求
,(1)求 的振幅,周期和初相;(2)求
的振幅,周期和初相;(2)求 值组成的集合。(3)求
值组成的集合。(3)求