题目内容
复数z=(1-i)a2-3a+2+i,(a∈R),
(1)若z为纯虚数,求z;
(2)若复平面内复数z对应的点在第三象限,求a的取值范围.
(1)若z为纯虚数,求z;
(2)若复平面内复数z对应的点在第三象限,求a的取值范围.
分析:(1)由条件可得
,由此求得z的值.
(2)由题知,
,由此解得a的范围.
|
(2)由题知,
|
解答:解:(1)∵z=(1-i)a2-3a+2+i=a2-3a+2+(1-a2)i,(a∈R),
则由z为纯虚数可得
,解得a=2,a=1(舍去)∴z=-3i.---------(6分)
(2)由题知,
,解得
,
即 1<a<2,故a的范围为(1,2).-----(12分)
则由z为纯虚数可得
|
(2)由题知,
|
|
即 1<a<2,故a的范围为(1,2).-----(12分)
点评:本题主要考查复数的基本概念,复数的代数表示及其几何意义,复数与复平面内对应点之间的关系,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
若复数z(1-i)=a+3i(i是虚数单位,a是实数),且z=
(
为共轭的复数),则a=( )
. |
| z |
. |
| z |
| A、2 | ||
B、
| ||
| C、3 | ||
| D、-3 |
 (
( 为z的共轭复数),则a= .
为z的共轭复数),则a= .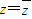 (
( 为共轭的复数),则a=( )
为共轭的复数),则a=( )