题目内容
已知函数f(x)=2x+1,g(x)=x2-2x+1
(1)设集合A={x|g(x)=9},求集合A;
(2)若x∈[-2,5],求g(x)的值域;
(3)画出y=
的图象,写出其单调区间.
(1)设集合A={x|g(x)=9},求集合A;
(2)若x∈[-2,5],求g(x)的值域;
(3)画出y=
|
分析:(1)解一元二次方程g(x)=9,即x2-2x-8=0,求出集合A.
(2)利用二次函数的性质求出g(x)=(x-1)2,在闭区间[-2,5]上的最值.
(3)画出y=
的图象,结合图象写出其单调区间.
(2)利用二次函数的性质求出g(x)=(x-1)2,在闭区间[-2,5]上的最值.
(3)画出y=
|
解答:解:(1)A={x|g(x)=9}={x|x2-2x-8=0}={-2,4}.…(4分)
(2)g(x)=(x-1)2,∵x∈[-2,5],
当x=1时,g(x)min=0.…6 分
当x=5时,g(x)max=16.…(9分)
(3)画出图象: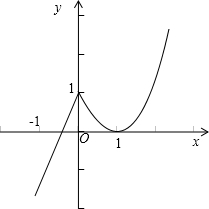 …(12分)
…(12分)
由图象可得单调增区间是(-∞,0]和[1,+∞),…(13分)
单调减区间是[0,1].…(14分)
(2)g(x)=(x-1)2,∵x∈[-2,5],
当x=1时,g(x)min=0.…6 分
当x=5时,g(x)max=16.…(9分)
(3)画出图象:
 …(12分)
…(12分)由图象可得单调增区间是(-∞,0]和[1,+∞),…(13分)
单调减区间是[0,1].…(14分)
点评:本题主要考查函数的单调性的判断和证明,求函数的值域,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目