题目内容
在正四棱锥P-ABCD中,PA=
| ||
| 2 |
分析:根据正四棱锥P-ABCD中,PA=
AB,M是BC的中点,利用勾股定理即可求出PM与AB的关系,利用勾股定理证明PM⊥PN,利用线面垂直的判定定理可证PM⊥面PAD,因此可求平面PAD中经过G点且与直线PM垂直的直线的条数.
| ||
| 2 |
解答: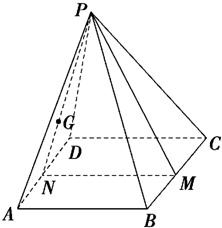 解:设正四棱锥的底面边长为a,则侧棱长为
解:设正四棱锥的底面边长为a,则侧棱长为
a.
由PM⊥BC,
∴PM=
a.
连接PG并延长与AD相交于N点
则PN=
a,MN=AB=a,
∴PM2+PN2=MN2,
∴PM⊥PN,又PM⊥AD,
∴PM⊥面PAD,
∴在平面PAD中经过G点的任意一条直线都与PM垂直.
故答案为无数.
 解:设正四棱锥的底面边长为a,则侧棱长为
解:设正四棱锥的底面边长为a,则侧棱长为
| ||
| 2 |
由PM⊥BC,
∴PM=
| ||
| 2 |
连接PG并延长与AD相交于N点
则PN=
| ||
| 2 |
∴PM2+PN2=MN2,
∴PM⊥PN,又PM⊥AD,
∴PM⊥面PAD,
∴在平面PAD中经过G点的任意一条直线都与PM垂直.
故答案为无数.
点评:此题是个中档题.考查直线与平面垂直的判断和性质定理,以及空间中直线的位置关系,学生利用知识分析解决问题的能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

