题目内容
16.已知函数f(x)=$\frac{x+b}{1+{x}^{2}}$是定义在(-1,1)上的奇函数.(1)求函数f(x)的解析式;
(2)用单调性的定义证明函数f(x)在(-1,1)上是增函数;
(3)解不等式f(2x-1)+f(x)<0.
分析 (1)利用奇函数的定义,求出b,即可求函数f(x)的解析式;
(2)根据单调性的定义证明函数f(x)在(-1,1)上是增函数;
(3)f(2x-1)+f(x)<0可化为-1<2x-1<-x<1,即可解不等式 f(2x-1)+f(x)<0.
解答 解:(1)∵函数f(x)=$\frac{x+b}{1+{x}^{2}}$是定义在(-1,1)上的奇函数,
∴f(0)=0,即b=0,
∴f(x)=$\frac{x}{1+{x}^{2}}$;
(2)设0<x1<x2<1,△x=x2-x1>0,
则△y=f(x2)-f(x1)=$\frac{{x}_{2}}{1+{{x}_{2}}^{2}}$-$\frac{{x}_{1}}{1+{{x}_{1}}^{2}}$=$\frac{{({x}_{1}-x}_{2})({{{x}_{1}x}_{2}-1)}^{\;}}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}$,
∵0≤x1<x2<1,
∴x2-x1>0,1-x1x2>0
∴f(x2)-f(x1)>0
∴f(x)在[0,1)上是增函数,
∵函数f(x)是定义在(-1,1)上的奇函数,
∴函数f(x)在(-1,1)上是增函数;
(3)f(2x-1)+f(x)<0可化为-1<2x-1<-x<1,
解得:0<x<$\frac{1}{3}$
∴不等式的解集为{x|0<x<$\frac{1}{3}$}.
点评 本题考查函数的奇偶性、单调性,考查解不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.函数$f(x)=\frac{{2\sqrt{x}}}{x+1}$的最大值为( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | 4 |
1.已知点A(2,3)与点B(6,y)的距离等于4$\sqrt{5}$,则y的值是( )
| A. | 11或5 | B. | -5或-11 | C. | 11 | D. | 11或-5 |
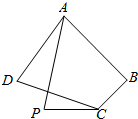 如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.
如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+4$\overrightarrow{CB}$•$\overrightarrow{CD}$=0.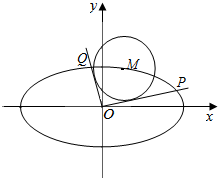 如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P、Q.