题目内容
(本小题满分13分)设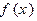 是定义在
是定义在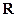 上的函数,对任意实数
上的函数,对任意实数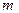 、
、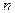 ,都有
,都有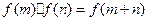 ,且当
,且当 <0时,
<0时,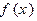 >1.
>1.
(1)证明:①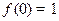 ;
;
②当 >0时,0<
>0时,0<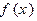 <1;
<1;
③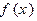 是
是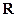 上的减函数;
上的减函数;
(2)设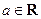 ,试解关于
,试解关于 的不等式
的不等式 ;
;
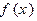 是定义在
是定义在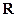 上的函数,对任意实数
上的函数,对任意实数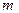 、
、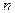 ,都有
,都有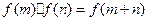 ,且当
,且当 <0时,
<0时,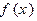 >1.
>1.(1)证明:①
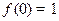 ;
;②当
 >0时,0<
>0时,0<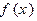 <1;
<1;③
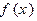 是
是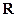 上的减函数;
上的减函数;(2)设
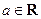 ,试解关于
,试解关于 的不等式
的不等式 ;
;(1)略
(2)当2<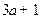 ,即
,即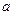 >
>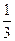 时,不等式的解集为
时,不等式的解集为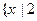 ≤
≤ ≤
≤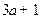
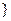 ;
;
当2=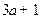 ,即
,即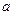 =
=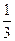 时,
时,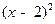 ≤0,不等式的解集为
≤0,不等式的解集为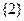 ;
;
当2>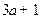 ,即
,即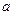 <
<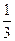 时,不等式的解集为
时,不等式的解集为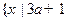 ≤
≤ ≤2
≤2 .
.
(2)当2<
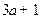 ,即
,即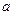 >
>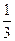 时,不等式的解集为
时,不等式的解集为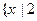 ≤
≤ ≤
≤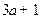
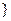 ;
;当2=
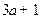 ,即
,即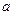 =
=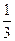 时,
时,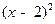 ≤0,不等式的解集为
≤0,不等式的解集为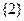 ;
;当2>
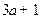 ,即
,即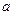 <
<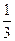 时,不等式的解集为
时,不等式的解集为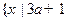 ≤
≤ ≤2
≤2 .
.解:(I)证明:(1)在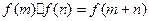 中,令
中,令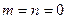
得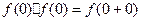 即
即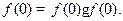 ∴
∴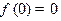 或
或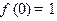 ,
,
若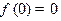 ,则当
,则当 <0时,有
<0时,有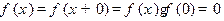 ,与题设矛盾,
,与题设矛盾,
∴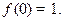
(2)当 >0时,
>0时,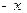 <0,由已知得
<0,由已知得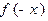 >1,
>1,
又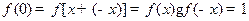 ,
,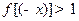 ,
,
∴ 0<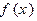 =
=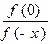 <1, 即
<1, 即 >0时,0<
>0时,0<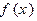 <1.
<1.
(3)任取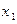 <
<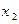 ,则
,则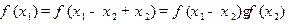 ,
,
∵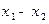 <0,∴
<0,∴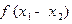 >1,又由(1)(2)及已知条件知
>1,又由(1)(2)及已知条件知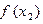 >0,
>0,
∴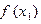 >
>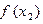 ,∴
,∴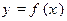 在定义域
在定义域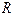 上为减函数.
上为减函数.
(II)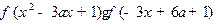 =
=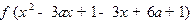
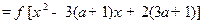
又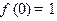 ,
,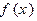 在
在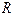 上单调递减.
上单调递减.
∴原不等式等价于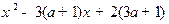 ≤0
≤0
不等式可化为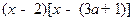 ≤0
≤0
当2<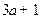 ,即
,即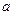 >
>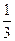 时,不等式的解集为
时,不等式的解集为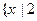 ≤
≤ ≤
≤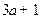
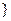 ;
;
当2=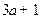 ,即
,即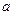 =
=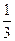 时,
时,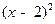 ≤0,不等式的解集为
≤0,不等式的解集为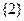 ;
;
当2>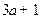 ,即
,即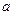 <
<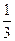 时,不等式的解集为
时,不等式的解集为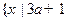 ≤
≤ ≤2
≤2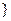 .
.
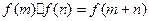 中,令
中,令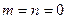
得
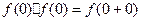 即
即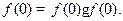 ∴
∴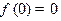 或
或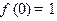 ,
,若
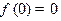 ,则当
,则当 <0时,有
<0时,有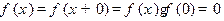 ,与题设矛盾,
,与题设矛盾,∴
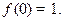
(2)当
 >0时,
>0时,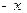 <0,由已知得
<0,由已知得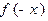 >1,
>1,又
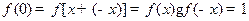 ,
,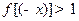 ,
,∴ 0<
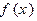 =
=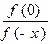 <1, 即
<1, 即 >0时,0<
>0时,0<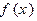 <1.
<1.(3)任取
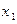 <
<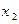 ,则
,则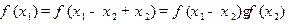 ,
,∵
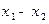 <0,∴
<0,∴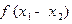 >1,又由(1)(2)及已知条件知
>1,又由(1)(2)及已知条件知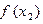 >0,
>0,∴
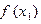 >
>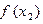 ,∴
,∴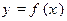 在定义域
在定义域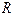 上为减函数.
上为减函数. (II)
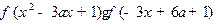 =
=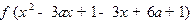
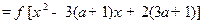
又
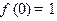 ,
,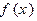 在
在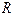 上单调递减.
上单调递减. ∴原不等式等价于
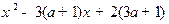 ≤0
≤0不等式可化为
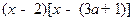 ≤0
≤0当2<
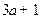 ,即
,即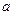 >
>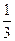 时,不等式的解集为
时,不等式的解集为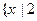 ≤
≤ ≤
≤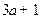
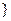 ;
;当2=
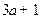 ,即
,即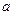 =
=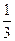 时,
时,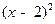 ≤0,不等式的解集为
≤0,不等式的解集为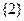 ;
;当2>
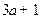 ,即
,即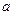 <
<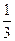 时,不等式的解集为
时,不等式的解集为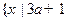 ≤
≤ ≤2
≤2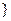 .
.
练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
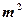 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度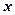 不得
不得 超过
超过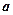 米,房屋正面的造价为400元
米,房屋正面的造价为400元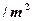 ,房屋侧面的造价为150元
,房屋侧面的造价为150元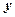 表示成
表示成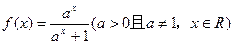 ,正项等比数列
,正项等比数列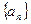 满足
满足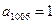 ,则
,则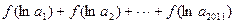 等于( )
等于( )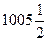
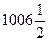
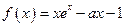 ,则关于
,则关于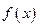 的零点叙述正确的是( ▲ )
的零点叙述正确的是( ▲ )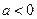 时,函数
时,函数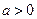 时,函数
时,函数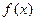 定义域中任意的
定义域中任意的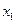 .
.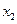 (
(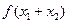 =
= 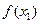
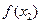 ; ②
; ②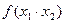 =
=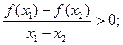 ④
④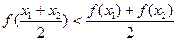
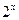 时,上述结论中正确结论的序号是 .
时,上述结论中正确结论的序号是 . 2x
2x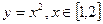 与函数
与函数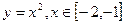 即为“同族函数”,请你找出下面哪个函数解析式也能够被用来构造“同族函数”的是( )
即为“同族函数”,请你找出下面哪个函数解析式也能够被用来构造“同族函数”的是( )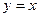
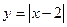
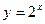
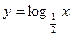
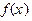 唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是( ).
唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是( ).  ,则
,则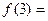 ( )
( )