题目内容
10.已知f(x)=$\left\{\begin{array}{l}{\frac{x}{{e}^{x}},x≥0}\\{-x.x<0}\end{array}\right.$,若关于x的方程f2(x)-mf(x)+m-1=0恰好有4个不相等的实数根,则实数m的取值范围为.| A. | ($\frac{1}{e}$,2)∪(2,e) | B. | ($\frac{1}{e}$,1) | C. | (1,$\frac{1}{e}$+1) | D. | ($\frac{1}{e}$,e) |
分析 由方程f2(x)-mf(x)+m-1=0可解得f(x)=1或f(x)=m-1;从而可得方程f(x)=m-1有3个不是-1的根;再分析函数f(x)的单调性及取值即可.
解答 解:解方程f2(x)-mf(x)+m-1=0得,
f(x)=1或f(x)=m-1;
解f(x)=1得x=-1,
故方程f(x)=m-1有3个不是-1的根;
当x≥0时,
f(x)=$\frac{x}{{e}^{x}}$,f′(x)=$\frac{1-x}{{e}^{x}}$;
故f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
f(0)=0,f(1)=$\frac{1}{e}$,$\underset{lim}{x→+∞}$$\frac{x}{{e}^{x}}$=0;
当x<0时,
f(x)=-x在(-∞,0)上是减函数,且+∞→0;
故若使方程f(x)=m-1有3个不是-1的根,
则0<k-1<$\frac{1}{e}$;
即$\frac{1}{e}$<k<1+$\frac{1}{e}$;
故选C.
点评 本题考查了导数的综合应用及分段函数的应用,属于中档题.

练习册系列答案
相关题目
5.准线方程为x=2的抛物线的标准方程是( )
| A. | y2=-4x | B. | y2=-8x | C. | y2=-x | D. | y2=8x |
20.已知集合A={x|y=log2(x-1),y∈N*,x∈B},B={2,3,4,5,6,7,8,9},则A∩B=( )
| A. | {1,2} | B. | {1,2,3} | C. | {3,5,9} | D. | {2,3,4,5,6,7,8,9} |
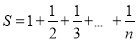 的值的程序框图.
的值的程序框图.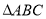 中,三个内角
中,三个内角 成等差数列,且
成等差数列,且 .
.
 ,点
,点 ,若函数
,若函数 的图象经过
的图象经过 三点,且
三点,且 为
为 的图象与
的图象与 轴相邻的两个交点,求
轴相邻的两个交点,求 的解析式.
的解析式. ,则函数
,则函数 的最小正周期与最大值分别为( )
的最小正周期与最大值分别为( ) B.
B.
 D.
D.