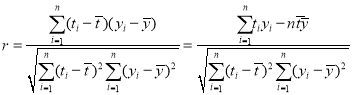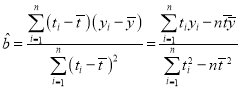题目内容
【题目】在直角坐标系
中，曲线
的参数方程为
，若曲线
与曲线关于直线
对称.
（1）求曲线的直角坐标方程；
（2）在以
为极点，
轴的正半轴为极轴的极坐标系中，射线
与的异于极点的交点为
，与的异于极点的交点为
，求
.
【答案】（1）
；（2）
.
【解析】
（1）求出曲线
的直角坐标方程，根据对称性即可求得曲线
的直角坐标方程；
（2）分别写出两个曲线的极坐标方程，求出直线与曲线的交点的极坐标，根据几何意义即可求解.
（1）曲线的参数方程为
，
化为直角坐标方程：
，即圆心坐标
，半径为2的圆，
曲线与曲线关于直线
对称，曲线也是半径为2的圆，设圆心坐标
，
有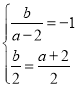
，解得
，所以
，
曲线的直角坐标方程；
（2）曲线是圆心坐标，半径为2的圆，其极坐标方程为：
，
曲线是圆心坐标，半径为2的圆，极坐标方程为：
，
射线
与的异于极点的交点为
，与的异于极点的交点为
，
所以
，
.
名校课堂系列答案
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销，得到一组数据
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
（1）试根据4月2日、3日、4日的三组数据，求
关于
的线性回归方程
，并预测4月6日的产品销售量
；
（2）若选取两组数据确定回归方程，求选取得两组数据恰好是不相邻两天的事件
的概率.
参考公式：
其中
，
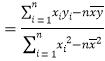【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本，其选报文科理科的情况如下表所示．
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
（Ⅰ）若在该样本中从报考文科的学生中随机地选出3人召开座谈会，试求3人中既有男生也有女生的概率；
（Ⅱ）用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关？
参考公式和数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
