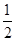题目内容
已知三个正数a,b,c满足a<b<c.
(Ⅰ)若a,b,c是从1,2,3,4,5中任取的三个数,求a,b,c能构成三角形三边长的概率;
(Ⅱ)若a,b,c是从区间(0,1)内任取的三个数,求a,b,c能构成三角形三边长的概率.
(Ⅰ)若a,b,c是从1,2,3,4,5中任取的三个数,求a,b,c能构成三角形三边长的概率;
(Ⅱ)若a,b,c是从区间(0,1)内任取的三个数,求a,b,c能构成三角形三边长的概率.
(Ⅰ)首先任选3个数,共有C53=10种情况,
其中能构成三角形的有2,3,4;2,4,5;3,4,5三种情况,
故能构成三角形三边的概率是
.
(Ⅱ)记Ω={(a,b,c)|
},a,b,c能构成三角形三边长为事件A,
则A={(a,b,c)|
}
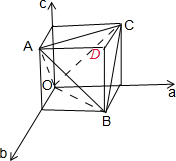
在空间直角坐标系oabc内画出满足以上条件的区域,如图所示,
可求得正方体的体积是1,三棱锥O-ABC的体积与三棱锥D-ABC和是
,
由几何概型的计算得,
从区间(0,1)内任取的三个数a,b,c能构成三角形三边长的概率为P(A)=
=
=
其中能构成三角形的有2,3,4;2,4,5;3,4,5三种情况,
故能构成三角形三边的概率是
| 3 |
| 10 |
(Ⅱ)记Ω={(a,b,c)|
|
则A={(a,b,c)|
|
在空间直角坐标系oabc内画出满足以上条件的区域,如图所示,
可求得正方体的体积是1,三棱锥O-ABC的体积与三棱锥D-ABC和是
| 1 |
| 2 |
由几何概型的计算得,
从区间(0,1)内任取的三个数a,b,c能构成三角形三边长的概率为P(A)=
| VO-ABC+VD-ABC |
| 正方体的体积 |
| ||
| 1 |
| 1 |
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
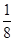 B.
B.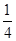 C.
C. D .
D .