题目内容
设0≤x≤2,求当x为何值时,函数y=4x-
-2x+1+5取最大值,并求出最大值.
| 1 | 2 |
分析:通过x的范围,求出2x的范围,化简函数的表达式,配方后求解最大值.
解答:解:∵0≤x≤2,∴1≤2x≤4,
函数y=4x-
-2x+1+5
=
(2x)2-2•2x+5
=
(2x-2)2+3,1≤2x≤4,
所以当2x=2,即x=1时,函数有最小值:3.
当2x=4,即x=2时,函数有最大值:5.
∴x=2时函数的最小值为:5.
函数y=4x-
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
所以当2x=2,即x=1时,函数有最小值:3.
当2x=4,即x=2时,函数有最大值:5.
∴x=2时函数的最小值为:5.
点评:本题考查二次函数的最大值的求法,配方法的应用,基本知识的考查.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
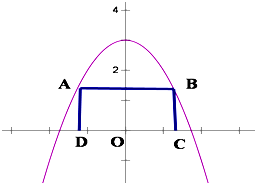 如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).
如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).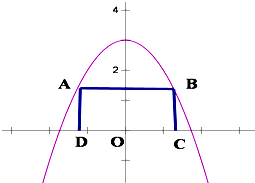 如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).
如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).