题目内容
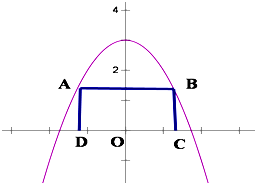 如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).
如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).(1)写出函数S(x)的解析式,并求出函数的定义域
(2)求当x为何值时,矩形ABCD的面积最大?并求出最大面积.
分析:(1)由A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧),可分别求出矩形的长和宽,代入矩形面积公式可得答案,结合B,C点均在Y轴右侧,求出曲线y=3-x2与X轴的交点坐标,可分析出函数的定义域
(2)由(1)中解析式,求出函数S(x)导函数的解析式,利用导数法,分析函数S(x)的单调性后,即可求出最大值.
(2)由(1)中解析式,求出函数S(x)导函数的解析式,利用导数法,分析函数S(x)的单调性后,即可求出最大值.
解答:解:(1)∵A是曲线y=3-x2(y>0)上的一个动点
若|OC|=x,即A的横坐标为-x时,A的纵坐标为3-x2,
故矩形ABCD的长和宽分别为2x,3-x2,
∴S(x)=2x(3-x2)
又∵曲线y=3-x2与x正半轴交于(
,0)点
故x∈(0,
)
即函数的定义域为(0,
)
(2)S(x)=2x(3-x2)=-2x3+6x
∴S′(x)=-6x2+6,x∈(0,
)
令S′(x)=0,则x=1
∵x∈(0,1)时,S′(x)>0,
x∈(1,
)时,S′(x)<0,
故当x=1时面积最大,最大面积为4
若|OC|=x,即A的横坐标为-x时,A的纵坐标为3-x2,
故矩形ABCD的长和宽分别为2x,3-x2,
∴S(x)=2x(3-x2)
又∵曲线y=3-x2与x正半轴交于(
| 3 |
故x∈(0,
| 3 |
即函数的定义域为(0,
| 3 |
(2)S(x)=2x(3-x2)=-2x3+6x
∴S′(x)=-6x2+6,x∈(0,
| 3 |
令S′(x)=0,则x=1
∵x∈(0,1)时,S′(x)>0,
x∈(1,
| 3 |
故当x=1时面积最大,最大面积为4
点评:本题考查的知识点是根据实际问题选择函数类型,利用导数求闭区间上函数的最值,其中分析矩形的长和宽是解答本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线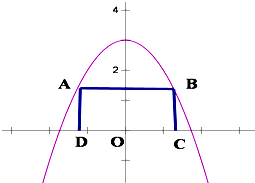 如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).
如图3,点A是曲线y=3-x2(y>0)上的一个动点(点A在y轴左侧)以点A为顶点作矩形ABCD,使点B在此曲线上,D,C在x轴上,设|OC|=x,矩形ABCD的面积为S(x).
 的距离的最小值是 .
的距离的最小值是 . 的最小值是 .
的最小值是 .