题目内容
设当x=θ时,函数f(x)=3sinx+4cosx取得最小值,则cosθ=______.
由f(x)=3sinx+4cosx
=5(
sinx+
cosx),
令cosα=
,sinα=
,
∴f(x)=5(sinxcosα+cosxsinα)
=5sin(x+α).
当x+α=-
+2kπ,k∈Z时,
即θ=x=-
-α+2kπ,k∈Z时,f(x)有最小值.
此时cosθ=cos(-
-α+2kπ)=-sinα=-
.
故答案为:-
.
=5(
| 3 |
| 5 |
| 4 |
| 5 |
令cosα=
| 3 |
| 5 |
| 4 |
| 5 |
∴f(x)=5(sinxcosα+cosxsinα)
=5sin(x+α).
当x+α=-
| π |
| 2 |
即θ=x=-
| π |
| 2 |
此时cosθ=cos(-
| π |
| 2 |
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |

练习册系列答案
相关题目
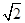 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2. 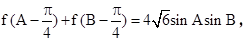 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.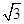 ,b=1,B=30°.(1)求角A; (2)求△ABC的面积.
,b=1,B=30°.(1)求角A; (2)求△ABC的面积.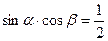 ,则
,则 范围 。
范围 。