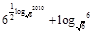题目内容
关于x的方程ax=-x2+2x+a(a>0,且a≠1)的解的个数是( )
| A.1 | B.2 | C.0 | D.视a的值而定 |
B
解析

练习册系列答案
相关题目
设 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意 ,都有
,都有 且
且
当 时,
时, 内关于x的方程
内关于x的方程 恰有3个不同的实数根,则a的取值范围是 ( )
恰有3个不同的实数根,则a的取值范围是 ( )
A. | B. | C.(1,2) | D. |
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则a的取值范围是 ( )
A.(-2,2 | B.(-∞,2 | C. -2,2 -2,2 | D.(-∞,-2) |
设函数f(x)=x2+2(a-1)x+2在区间(-∞, 上是减函数,则实数a的范围是
上是减函数,则实数a的范围是
| A.a≥-3 | B.a≤-3 | C.a≥3 | D.a≤5 |
50.6,0.65,log0.65的大小顺序是( )
| A.0.65<log0.65<50.6 |
| B.0.65<50.6<log0.65 |
| C.log0.65<50.6<0.65 |
| D.log0.65<0.65<50.6 |
与函数 的图象相同的函数是 ( )
的图象相同的函数是 ( )
| A.y = x-1 | B.y =  | C.y = |x-1| | D.y = |
若logm9<logn9<0,那么m,n满足的条件是( )
| A.m>n>1 | B.0<n<m<1 | C.n>m>1 | D.0<m<n<1 |
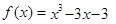 有零点的区间是( )
有零点的区间是( )