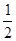题目内容
设函数f(x)=x2+2(a-1)x+2在区间(-∞, 上是减函数,则实数a的范围是
上是减函数,则实数a的范围是
| A.a≥-3 | B.a≤-3 | C.a≥3 | D.a≤5 |
B
解析

练习册系列答案
相关题目
如果指数函数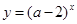 在
在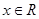 上是减函数,则a的取值范围是
上是减函数,则a的取值范围是
| A.a>2 | B.0<a<1 | C.2<a<3 | D.a>3 |
设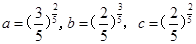 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
| A.a>c>b | B.a>b>c |
| C.c>a>b | D.b>c>a |
计算 的结果是( )
的结果是( )
A. | B. | C.1 | D.2 |
物体A以速度v=3t 2+1(m/s)在一直线l上运动,物体B在直线l上,且在物体A的正前方5 m处,同时以v=10t(m/s)的速度与A同向运动,出发后物体A追上物体B所用的时间t(s)为 ( )
| A.3 | B.4 | C.5 | D.6 |
关于x的方程ax=-x2+2x+a(a>0,且a≠1)的解的个数是( )
| A.1 | B.2 | C.0 | D.视a的值而定 |
设奇函数 在
在 上是增函数,且
上是增函数,且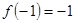 ,当
,当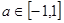 时,
时,  对所有的
对所有的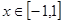 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A. 或 或 或 或 | B. 或 或 |
C. 或 或 或 或 | D. |
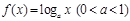 在区间
在区间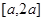 上的最大值是最小值的
上的最大值是最小值的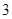 倍,则
倍,则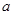 的值为( )
的值为( )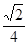 B.
B. 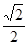 C.
C. 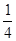 D.
D.