题目内容
已知函数f(x)=x(x-c)2在x=2处有极大值.(1)求c的值;
(2)若x∈[0,9],求函数f(x)的最值
(3)是否存在实数k,使得对?x1,x2∈[0,9]恒有f(x1)-f(x2)<k成立?若存在,求出k的取值范围;若不存在,请说明理由.
分析:(1)由函数在x=2处有极大值得到f′(x)=(x-c)2+2x(x-c)=0解出c的值即可;
(2)在区间[0,9]上,利用c的值加上函数的驻点来分区间讨论函数的增减性得到函数的最值;
(3)对?x1,x2∈[0,9]恒有f(x1)-f(x2)<k成立意思是当k大于f(x1)-f(x2)的最大值即为恒成立,即当f(x1)最大,f(x2)最小时f(x1)-f(x2)有最大值,即可得到k的取值范围.
(2)在区间[0,9]上,利用c的值加上函数的驻点来分区间讨论函数的增减性得到函数的最值;
(3)对?x1,x2∈[0,9]恒有f(x1)-f(x2)<k成立意思是当k大于f(x1)-f(x2)的最大值即为恒成立,即当f(x1)最大,f(x2)最小时f(x1)-f(x2)有最大值,即可得到k的取值范围.
解答:解:(1)函数f(x)=x(x-c)2在x=2处有极大值,
令f′(x)=(x-c)2+2x(x-c)=0得到x=c或x=
,
则c=2或c=6;
(2)由c=6得f(x)=x(x-6)2,f′(x)=3(x-6)(x-2)
当f′(x)>0即x∈[0,2)∪(6,9],f(x)为递增函数;当f′(x)<0即x∈(2,6)时,f(x)为递减函数.
所以f(x)max=f(2)=32,f(x)min=f(6)=0;
由c=2得f(x)=x(x-2)2,f′(x)=3(x-
)(x-2)
当f′(x)>0即x∈[0,
)∪(2,9],f(x)为递增函数;当f′(x)<0即x∈(
,2)时,f(x)为递减函数.
所以f(x)max=f(
)=
,f(x)min=f(2)=0;
(3)找出f(x1)-f(x2)的最大值,当c=6时,f(x1)-f(x2)=f(x)max-f(x)min=32-0=32,则k>32;
当c=2时,f(x1)-f(x2)=f(x)max-f(x)min=
,则k>
令f′(x)=(x-c)2+2x(x-c)=0得到x=c或x=
| c |
| 3 |
则c=2或c=6;
(2)由c=6得f(x)=x(x-6)2,f′(x)=3(x-6)(x-2)
当f′(x)>0即x∈[0,2)∪(6,9],f(x)为递增函数;当f′(x)<0即x∈(2,6)时,f(x)为递减函数.
所以f(x)max=f(2)=32,f(x)min=f(6)=0;
由c=2得f(x)=x(x-2)2,f′(x)=3(x-
| 2 |
| 3 |
当f′(x)>0即x∈[0,
| 2 |
| 3 |
| 2 |
| 3 |
所以f(x)max=f(
| 2 |
| 3 |
| 32 |
| 27 |
(3)找出f(x1)-f(x2)的最大值,当c=6时,f(x1)-f(x2)=f(x)max-f(x)min=32-0=32,则k>32;
当c=2时,f(x1)-f(x2)=f(x)max-f(x)min=
| 32 |
| 27 |
| 32 |
| 27 |
点评:考查学生利用导数研究函数极值的能力,利用导数求闭区间上函数最值的能力.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
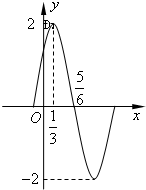 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|