Question

已知数列a_n是首项为1，公比为2的等比数列，f（n）=a₁C_n¹+a₂C_n²+…+a_kC_n^k+…+a_nC_nⁿ（n∈N^*）则f（n）=________．

Answer 1

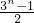
分析：根据题意写出f（n）=a₁C_n¹+a₂C_n²+…+a_kC_n^k+…+a_nC_nⁿ（n∈N^*），再由组合数的性质将其形式进行变化，利用二项式定理进行化简求值
解答：∵数列a_n是首项为1，公比为2的等比数列，
∴f（n）=a₁C_n¹+a₂C_n²+…+a_kC_n^k+…+a_nC_nⁿ（n∈N^*）
=1×C_n¹+2×C_n²+…+2^k-1C_n^k+…+2^n-1C_nⁿ
=（2×C_n^n-1+2²×C_n^n-2+…+2^kC_n^n-k+…+2ⁿC_n⁰）
=（1×C_nⁿ+2×C_n^n-1+2²×C_n^n-2+…+2^kC_n^n-k+…+2ⁿC_n⁰）-
=（1+2）ⁿ-
=
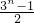
故答案为
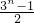
点评：本题考查二项式定理的应用，解题的关键是根据题设中所给的条件对f（n）进行恒等变形，转化为可以利用二项式化简的形式来，本题对观察能力要求较高，根据题设条件结合所学的知识对问题灵活变形，是高中数学的重要能力，转化化归的能力，题后应通过本题好好体会一下．本题易因为知识缺陷导致找不到转化的方向而出错，对基础知识一定要掌握牢固，理解透彻．