题目内容
点集C1,C2,C3,C4分别对应函数f1(x)=
,f2(x)=
,f3(x)=
,f4(x)=
的图象上的点的集合,给出以下四个命题:
(1)C1⊆C2;
(2)C4⊆C3;
(3)C1∪C3=C2∪C4;
(4)C1∩C3=C2∩C4,
其中正确命题的序号是
| x+4 |
| 4+|x| |
| 4-x |
| 4-|x| |
(1)C1⊆C2;
(2)C4⊆C3;
(3)C1∪C3=C2∪C4;
(4)C1∩C3=C2∩C4,
其中正确命题的序号是
(4)
(4)
.分析:分别将函数进行化简,通过判断函数解析式之间的关系判断点集之间的关系即可.
解答:解:函数f1(x)=
定义域为{x|x≥-4}.(对应的点集为图1)
函数f2(x)=
=
,(对应的点集为图2)
函数f3(x)=
定义域为{x|x≤4},(对应的点集为图3)
函数f4(x)=
=
.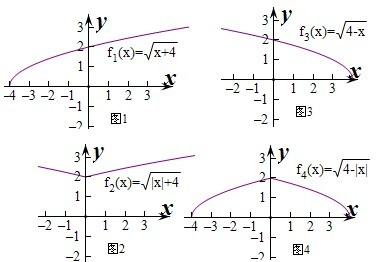 (对应的点集为图4)
(对应的点集为图4)
所以(1)C1⊆C2,错误.
(2)C4⊆C3;错误.
(3)C1∪C3=C2∪C4;错误.
(4)C1∩C3=C2∩C4={(0,2)}正确.
故答案为:(4)
| x+4 |
函数f2(x)=
| 4+|x| |
|
函数f3(x)=
| 4-x |
函数f4(x)=
| 4-|x| |
|
 (对应的点集为图4)
(对应的点集为图4)所以(1)C1⊆C2,错误.
(2)C4⊆C3;错误.
(3)C1∪C3=C2∪C4;错误.
(4)C1∩C3=C2∩C4={(0,2)}正确.
故答案为:(4)
点评:本题主要考查函数的图象以及图象之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
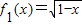 ,
,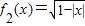 ,
,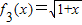 ,
,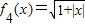 的图象分别是点集C1,C2,C3,C4,这些图象关于直线x=0的对称曲线分别是点集D1,D2,D3,D4,现给出下列四个命题,其中正确命题的序号是( )
的图象分别是点集C1,C2,C3,C4,这些图象关于直线x=0的对称曲线分别是点集D1,D2,D3,D4,现给出下列四个命题,其中正确命题的序号是( )