题目内容
已知 、
、 是两个非零向量,且满足|
是两个非零向量,且满足| |=|
|=| |=|
|=| -
- |,求:
|,求:(1)
 与
与 +
+ 的夹角;
的夹角;(2)求
 的值.
的值.
【答案】分析:(1)由条件|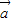 |=|
|=|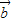 |=|
|=|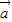 -
-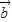 |,可得
|,可得 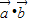 =
=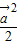 =
=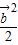 ,可得|
,可得|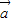 +
+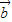 |=
|=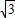 |
|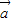 |.再利用两个向量的夹角公式求得cos<
|.再利用两个向量的夹角公式求得cos<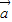 ,
,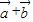 >=
>=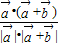 的
的
值,可得<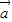 ,
,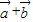 >的值..
>的值..
(2)根据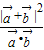 =
=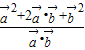 =
=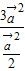 ,运算求得结果.
,运算求得结果.
解答:解:(1)由条件|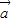 |=|
|=|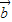 |=|
|=|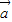 -
-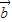 |,可得
|,可得 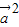 =
=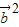 =
=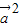 +
+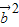 -2
-2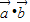 ,∴
,∴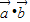 =
=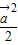 =
=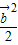 ,∴|
,∴|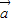 +
+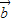 |=
|=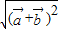 =
=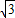 |
|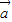 |.
|.
∴cos<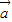 ,
,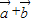 >=
>=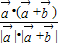 =
=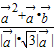 =
=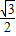 ,∴<
,∴<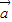 ,
,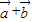 >=30°.
>=30°.
(2)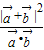 =
=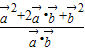 =
=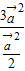 =6.
=6.
点评:本题主要考查两个向量的数量积的运算,两个向量的夹角公式的应用,属于中档题.
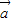 |=|
|=|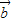 |=|
|=|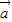 -
-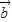 |,可得
|,可得 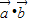 =
=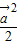 =
=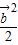 ,可得|
,可得|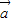 +
+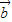 |=
|=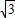 |
|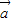 |.再利用两个向量的夹角公式求得cos<
|.再利用两个向量的夹角公式求得cos<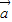 ,
,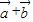 >=
>=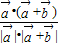 的
的值,可得<
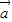 ,
,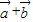 >的值..
>的值..(2)根据
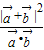 =
=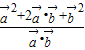 =
=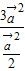 ,运算求得结果.
,运算求得结果.解答:解:(1)由条件|
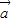 |=|
|=|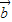 |=|
|=|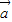 -
-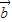 |,可得
|,可得 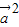 =
=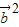 =
=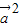 +
+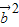 -2
-2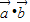 ,∴
,∴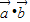 =
=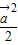 =
=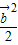 ,∴|
,∴|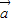 +
+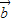 |=
|=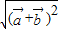 =
=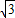 |
|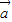 |.
|.∴cos<
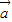 ,
,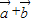 >=
>=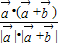 =
=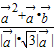 =
=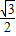 ,∴<
,∴<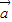 ,
,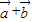 >=30°.
>=30°.(2)
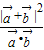 =
=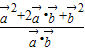 =
=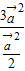 =6.
=6.点评:本题主要考查两个向量的数量积的运算,两个向量的夹角公式的应用,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 ,
, 是两个非零向量,当
是两个非零向量,当 +t
+t (t∈R)的模取最小值时,
(t∈R)的模取最小值时,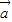 与
与 共线且同向,求证:
共线且同向,求证: 与
与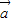 +t
+t 垂直.
垂直. ,
, 是两个非零向量,且|
是两个非零向量,且| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角大小为 .
的夹角大小为 .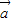 ,
,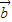 是两个非零向量,且
是两个非零向量,且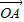 =
=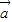 +
+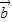 ,
,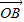 =
=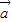 +2
+2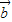 ,
,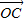 =
=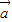 +3
+3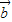 ,则
,则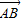 与
与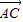 的夹角为 .
的夹角为 .