题目内容
已知直线l1经过点(-4,3)且与圆x2+y2=25相切,直线l2的方程为y=kx+5,若l1⊥l2,则k=( )A.

B.

C.
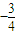
D.
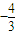
【答案】分析:由直线与圆相切的性质可求直线且l1的斜率,然后根据且l1⊥l2可求k
解答:解:由题意可知直线直线l1的斜率存在,可设直线方程为y-3=m(x+4)
由直线与圆相切的性质可知,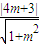 =5
=5
∴m=
∵直线l2的方程为y=kx+5,且l1⊥l
∴k=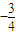
故选C
点评:本题主要考查了直线与圆相切性质的应用及两条直线垂直的斜率关系的应用,属于基础试题
解答:解:由题意可知直线直线l1的斜率存在,可设直线方程为y-3=m(x+4)
由直线与圆相切的性质可知,
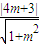 =5
=5∴m=

∵直线l2的方程为y=kx+5,且l1⊥l
∴k=
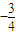
故选C
点评:本题主要考查了直线与圆相切性质的应用及两条直线垂直的斜率关系的应用,属于基础试题

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目