题目内容
．设函数
在区间
的导函数
，在区间的导函数
，若在区间上的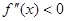
恒成立，则称函数
在区间上为“凸函数”，已知
，若当实数
满足
时，函数在区间上为“凸函数”，则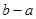
的最大值为（ ）
A．
B．
C．
D．
【答案】
D
【解析】当|m|≤2时，f″（x）=x2-mx-3＜0恒成立⇔当|m|≤2时，mx＞x2-3恒成立．（8分）
当x=0时，f″（x）=-3＜0显然成立．（9分）
当x＞0，x-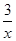
＜m
∵m的最小值是-2．
∴x-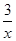＜-2．
从而解得0＜x＜1（11分）
当x＜0，x-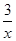＞m
∵m的最大值是2，∴x-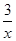 ＞2，
从而解得-1＜x＜0．（13分）
综上可得-1＜x＜1，从而（b-a）max=1-（-1）=2（14分）
故答案为： 2．
练习册系列答案
相关题目
在
上的导函数为
，
，若在
恒成立，则称函数
在
．
上的“凸函数”，试确定实数
的值；
时，函数
的最大值．
在区间
的导函数为
在区间
若在区间
恒成立，则称函数
在区间
，若对任意的实数m满足
时，函数
的最大值为（ ）
在区间
的导函数
，
，若在区间
恒成立，则称函数
在区间
，若当实数
满足
时，函数
的最大值为（ ）
B．
C．
D．
在
上的导函数为
，
．若在
恒成立，则称函数
在
．
上的“凸函数”，试确定实数
的值；
时，函数
的最大值．