题目内容
设函数 在区间
在区间 的导函数为
的导函数为 在区间
在区间 的导函数为
的导函数为 若在区间
若在区间 上
上 恒成立,则称函数
恒成立,则称函数 在区间
在区间 上为“凸函数”,已知
上为“凸函数”,已知 ,若对任意的实数m满足
,若对任意的实数m满足 时,函数
时,函数 在区间
在区间 上为“凸函数”,则
上为“凸函数”,则 的最大值为( )
的最大值为( )
A.4 B.3 C.2 D.1
【答案】
C
【解析】
试题分析:当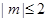 时,
时,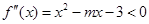 恒成立等价于当
恒成立等价于当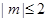 时,
时,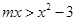 恒成立.当
恒成立.当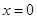 时,
时,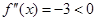 显然成立.
显然成立.
当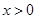 时,
时,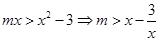 ,∵
,∵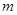 的最小值是-2,∴
的最小值是-2,∴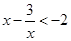 ,从而解得
,从而解得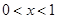 ;当
;当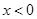 时,
时,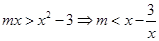 ,∵
,∵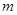 的最大值是2,∴
的最大值是2,∴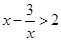 ,从而解得
,从而解得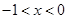 .综上可得
.综上可得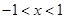 ,从而
,从而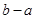 的最大值为
的最大值为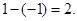
考点:本小题主要考查函数的导数与不等式恒成立问题的解法,考查知识迁移与转化能力.
点评:解决此类问题关键是要理解题目所给信息(新定义),另外恒成立问题一般要转化为最值问题解决,必要时要进行分类讨论.

练习册系列答案
相关题目
 在区间
在区间 的导函数
的导函数 ,
, ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数 在区间
在区间 ,若当实数
,若当实数 满足
满足 时,函数
时,函数 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 在区间
在区间 的导函数
的导函数 ,
, ,若在区间
,若在区间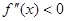 恒成立,则称函数
恒成立,则称函数 在区间
在区间 ,若当实数
,若当实数 满足
满足 时,函数
时,函数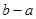 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 在
在 上的导函数为
上的导函数为 ,
, ,若在
,若在 恒成立,则称函数
恒成立,则称函数 在
在 .
. 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数 的值;
的值; 时,函数
时,函数 的最大值.
的最大值.