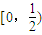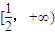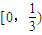题目内容
若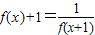 ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]内,g(x)=f(x)-m有两个零点,则实数m的取值范围是( )
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]内,g(x)=f(x)-m有两个零点,则实数m的取值范围是( )A.
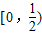
B.
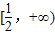
C.
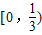
D.[0,1]
【答案】分析:先求函数的解析式,再分段考虑函数的零点,即可得出结论
解答:解:当x∈(-1,0),x+1∈(0,1),
∵当x∈[0,1]时,f(x)=x,
∴f(x+1)=x+1
∴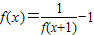 =
=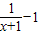
∴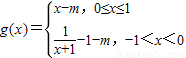
①当x∈[0,1]时,要使g(x)=0有解,必须有g(0)g(1)≤0,-m(1-m)≤0,
∴0≤m≤1
②当x∈(-1,0 )时,要使g(x)=0有解,必须有-1-m<0,∴m>-1
综上所述:0≤m≤1
故选D.
点评:本题考查函数的解析式,考查函数的零点,利用零点存在定理是关键.
解答:解:当x∈(-1,0),x+1∈(0,1),
∵当x∈[0,1]时,f(x)=x,
∴f(x+1)=x+1
∴
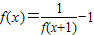 =
=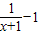
∴
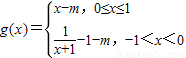
①当x∈[0,1]时,要使g(x)=0有解,必须有g(0)g(1)≤0,-m(1-m)≤0,
∴0≤m≤1
②当x∈(-1,0 )时,要使g(x)=0有解,必须有-1-m<0,∴m>-1
综上所述:0≤m≤1
故选D.
点评:本题考查函数的解析式,考查函数的零点,利用零点存在定理是关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
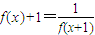 ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]内,g(x)=f(x)-m有两个零点,则实数m的取值范围是( )
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]内,g(x)=f(x)-m有两个零点,则实数m的取值范围是( )