题目内容
已知函数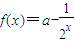 ,若f(x)为奇函数,则不等式
,若f(x)为奇函数,则不等式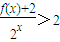 的解集为( )
的解集为( )A.(-∞,2)
B.(2,+∞)
C.(-∞,-2)
D.(-2,+∞)
【答案】分析:先根据函数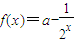 ,若f(x)为奇函数,求得a值.再根据不等式
,若f(x)为奇函数,求得a值.再根据不等式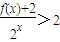 ,即f(x)+2>2x,最后解一个指数不等式即可得到答案.
,即f(x)+2>2x,最后解一个指数不等式即可得到答案.
解答:解:函数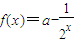 ,若f(x)为奇函数,
,若f(x)为奇函数,
∴f(0)=0,∴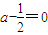 ,a=1;
,a=1;
∴函数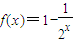 ,
,
不等式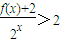 可化为:
可化为:
f(x)+2>2x即:3-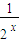 >2x,
>2x,
解得:x>2.
故选B.
点评:本题主要考查了函数单调性与奇偶性的应用.在已知函数的单调性求参数值时,常可利用f(0)=0来解决问题.
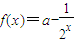 ,若f(x)为奇函数,求得a值.再根据不等式
,若f(x)为奇函数,求得a值.再根据不等式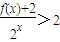 ,即f(x)+2>2x,最后解一个指数不等式即可得到答案.
,即f(x)+2>2x,最后解一个指数不等式即可得到答案.解答:解:函数
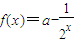 ,若f(x)为奇函数,
,若f(x)为奇函数,∴f(0)=0,∴
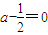 ,a=1;
,a=1;∴函数
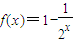 ,
,不等式
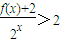 可化为:
可化为:f(x)+2>2x即:3-
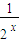 >2x,
>2x,解得:x>2.
故选B.
点评:本题主要考查了函数单调性与奇偶性的应用.在已知函数的单调性求参数值时,常可利用f(0)=0来解决问题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
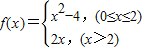 ,若f(x)=12,则x= .
,若f(x)=12,则x= .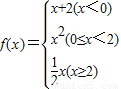 ,若f(x)=2,则x的值为( )
,若f(x)=2,则x的值为( )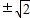
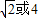
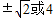
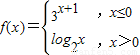 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .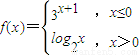 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .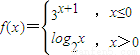 ,若f(x)≥1,则x的取值范围为 .
,若f(x)≥1,则x的取值范围为 .