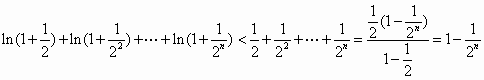题目内容
已知f(x)=lnx,g(x)=![]() x2+mx+
x2+mx+![]() (m<0),直线l与函数f(x)、g(x)的图像都相切,且与函数f(x)的图像的切点的横坐标为1.
(m<0),直线l与函数f(x)、g(x)的图像都相切,且与函数f(x)的图像的切点的横坐标为1.
(Ⅰ)求直线l的方程及m的值;
(Ⅱ)若h(x)=f(x+1)-![]() (x),求函数h(x)的最大值;
(x),求函数h(x)的最大值;
(Ⅲ)求证:对任意正整数n,总有![]() .
.
答案:
解析:
解析:
|
解:(Ⅰ)依题意知直线l的斜率 ∵ ∴直线l的方程为 又∵直线l与g(x)的图像也相切 ∴由 令 (Ⅱ) ∴ ∴ ∴ ∴当 (Ⅲ)∵由(II)知:当 ∴当 ∵ ∴ |

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
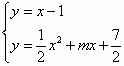 得
得