Question

(理)已知f(x)＝lnx－x²＋bx＋3

(1)若函数f(x)在点(2，y)处的切线与直线2x＋y＋2＝0垂直，求函数f(x)在区间[1，3]上的最小值；

(2)若f(x)在区间[1，m]上单调，求b的取值范围．

Answer 1

答案：
解析：

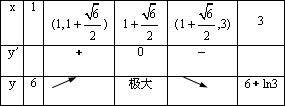
解：(1)　直线2x＋y＋2＝0斜率为－2 　　令(2)＝　得b＝4　　3分 　　f(x)＝lnx－x2＋4x＋3 　　　　5分 　　因为6＋ln3＞6　∴x＝1时　f(x)在[1，3]上最小值．　　8分 　　(2)令≥0得b≥2x－，在[1，m]上恒成立而 　　y＝2x－在[1，m]上单调递增，最大值为2m－ 　　∴b≥2m－　　12分 　　令≤0　得b≤2x－，在[1，m]上恒成立 　　而y＝2x－在[1，m]单调递增，最小值为y＝1 　　∴b≤1 　　故b≥2m－　或b≤1时f(x)在[1，m]上单调．　　16分