题目内容
设函数f(x)=
,若f(-2)=f(0),f(-1)=-3,则关于x的方程f(x)=x的解的个数是( )
|
| A、1 | B、2 | C、3 | D、4 |
分析:先求出函数f(x)的解析式,然后将方程f(x)=x的解的个数,转化成利用图象求两个函数图象的交点个数问题,作出函数y=f(x)与y=x的图象,从而得到结论.
解答:解:∵函数f(x)=
,f(-2)=f(0),f(-1)=-3,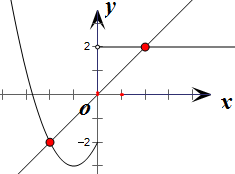
∴
,解得
,
∴f(x)=
,
关于x的方程f(x)=x的解的个数即为y=f(x)与y=x交点的个数,
作出函数y=f(x)与y=x的图象如右图
∴根据图象可知有2个交点,则方程f(x)=x的解的个数是2.
故选:B.
|

∴
|
|
∴f(x)=
|
关于x的方程f(x)=x的解的个数即为y=f(x)与y=x交点的个数,
作出函数y=f(x)与y=x的图象如右图
∴根据图象可知有2个交点,则方程f(x)=x的解的个数是2.
故选:B.
点评:本题考查了分段函数的图象,函数的零点与方程的关系,对于函数的零点,一般会转化成方程的根,或是利用图象转化成两个函数的交点问题.对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 设函数
设函数 设函数
设函数