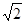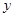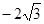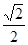题目内容
过点(0,-4)与曲线y=x3+x-2相切的直线方程是 ______.
【答案】
y=4x-4
【解析】主要考查导数公式、导数的几何意义及导数的四则运算法则。
解:设切点坐标为(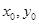 ),因为
),因为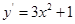 ,切线的斜率
,切线的斜率 ,又
,又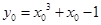 ,所以
,所以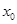 =1,
=1,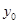 =1,切线斜率为4,故过点(0,-4)与曲线y=x3+x-2相切的直线方程是y=4x-4。
=1,切线斜率为4,故过点(0,-4)与曲线y=x3+x-2相切的直线方程是y=4x-4。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
.(本小题满分14分)
已知椭圆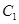 、抛物线
、抛物线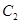 的焦点均在
的焦点均在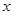 轴上,
轴上,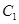 的中心和
的中心和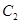 的顶点均为原点
的顶点均为原点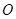 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求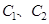 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线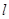 满足条件:①过
满足条件:①过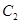 的焦点
的焦点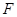 ;②与
;②与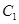 交不同两点
交不同两点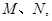 且满
且满
足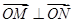 ?若存在,求出直线
?若存在,求出直线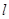 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
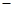 2
2