题目内容
设函数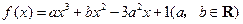 在
在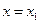 ,
,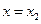 处取得极值,且
处取得极值,且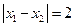 .
.
(Ⅰ)若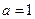 ,求
,求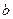 的值,并求
的值,并求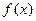 的单调区间;
的单调区间;
(Ⅱ)若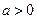 ,求
,求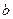 的取值范围.
的取值范围.
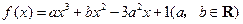 在
在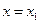 ,
,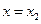 处取得极值,且
处取得极值,且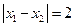 .
.(Ⅰ)若
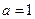 ,求
,求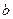 的值,并求
的值,并求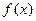 的单调区间;
的单调区间;(Ⅱ)若
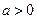 ,求
,求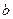 的取值范围.
的取值范围.解: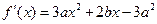 .①····················································· 2分
.①····················································· 2分
(Ⅰ)当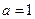 时,
时,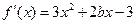 ;
;
由题意知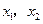 为方程
为方程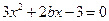 的两根,所以
的两根,所以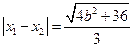 .
.
由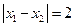 ,得
,得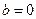 .········································································· 4分
.········································································· 4分
从而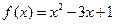 ,
,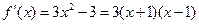 .
.
当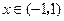 时,
时,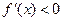 ;当
;当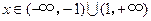 时,
时, .
.
故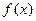 在
在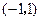 单调递减,在
单调递减,在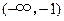 ,
,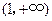 单调递增.····························· 6分
单调递增.····························· 6分
(Ⅱ)由①式及题意知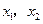 为方程
为方程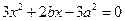 的两根,
的两根,
所以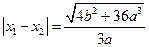 .从而
.从而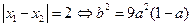 ,
,
由上式及题设知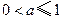 .······································································· 8分
.······································································· 8分
考虑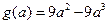 ,
,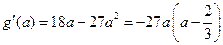 .………………………10分
.………………………10分
故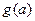 在
在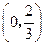 单调递增,在
单调递增,在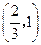 单调递减,从而
单调递减,从而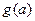 在
在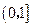 的极大值为
的极大值为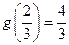 .
.
又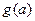 在
在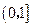 上只有一个极值,所以
上只有一个极值,所以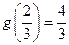 为
为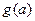 在
在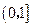 上的最大值,且最小值为
上的最大值,且最小值为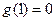 .所以
.所以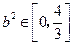 ,即
,即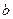 的取值范围
的取值范围
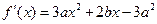 .①····················································· 2分
.①····················································· 2分(Ⅰ)当
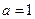 时,
时,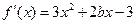 ;
;由题意知
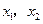 为方程
为方程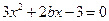 的两根,所以
的两根,所以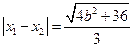 .
.由
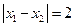 ,得
,得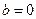 .········································································· 4分
.········································································· 4分从而
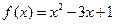 ,
,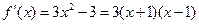 .
.当
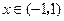 时,
时,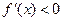 ;当
;当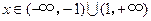 时,
时, .
.故
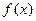 在
在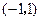 单调递减,在
单调递减,在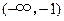 ,
,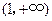 单调递增.····························· 6分
单调递增.····························· 6分(Ⅱ)由①式及题意知
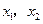 为方程
为方程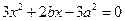 的两根,
的两根,所以
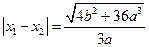 .从而
.从而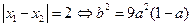 ,
,由上式及题设知
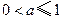 .······································································· 8分
.······································································· 8分考虑
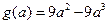 ,
,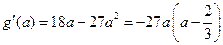 .………………………10分
.………………………10分故
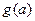 在
在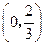 单调递增,在
单调递增,在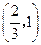 单调递减,从而
单调递减,从而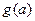 在
在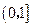 的极大值为
的极大值为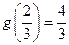 .
.又
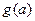 在
在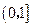 上只有一个极值,所以
上只有一个极值,所以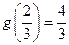 为
为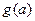 在
在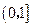 上的最大值,且最小值为
上的最大值,且最小值为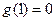 .所以
.所以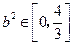 ,即
,即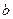 的取值范围
的取值范围略

练习册系列答案
相关题目
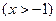 .
.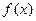 在其定义域上是单调函数,求实数
在其定义域上是单调函数,求实数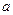 的取值范围;
的取值范围; 其定义域上既
其定义域上既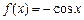 ,
,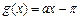 .
.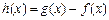 在
在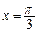 时取得极值,求
时取得极值,求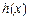 的单调递减区间;
的单调递减区间;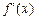 |≤| x |;
|≤| x |;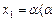 ∈[
∈[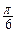 ,
,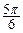 ]),
]),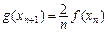 ,求证:
,求证: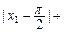
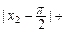 …+
…+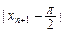 <
<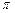 (n∈N*).
(n∈N*).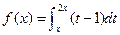 ,则
,则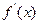 =" "
=" " 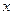 轴和
轴和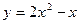 所围成的图形的面积为( )
所围成的图形的面积为( )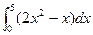
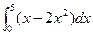
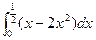
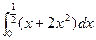
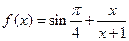
 ,则
,则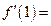
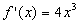 ,f(2 )=14,则此函数为 ( )
,f(2 )=14,则此函数为 ( )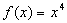
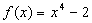
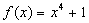
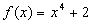
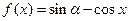 ,则
,则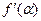 等于( )
等于( )