题目内容
已知双曲线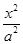 -
-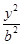 =1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线离心率e的最大值为________.
【答案】
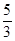
【解析】
试题分析:解法一:∵
∴
在△PF1F2中,由余弦定理得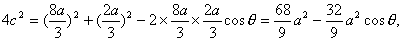
两边同时除以a2,得
又cos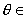 (-1,1),∴4<4e2<
(-1,1),∴4<4e2<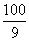 ,1<e<
,1<e<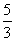 .
.
当点P、F1、F2共线时,θ=180°,e=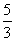 ,则1<e≤
,则1<e≤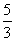 ,e的最大值为
,e的最大值为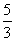 .
.
解法二:由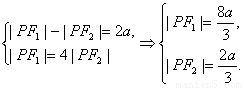
设|PP′|为点P到准线的距离,
∴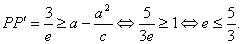
考点:本题主要考查双曲线的定义及其几何性质,余弦定理。
点评:基础题,由于题目条件中出现了曲线上的点到焦点的距离,易于想到运用双曲线定义。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
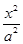 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
. ·
· =-23,求直线m的方程.
=-23,求直线m的方程. -
- =1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围.
=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围. -
- =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)