题目内容
已知双曲线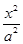 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
.
(1)求双曲线的方程;
(2)过点B作直线m交双曲线于M、N两点,若 ·
· =-23,求直线m的方程.
=-23,求直线m的方程.
【答案】
(1)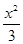 -y2=1;(2)y=
-y2=1;(2)y=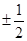 x-1.
x-1.
【解析】本试题主要考查双曲线的性质和方程的求解和运用,并利用向量为工具,求解直线与双曲线的位置关系的综合运用。
解:(1)依题意,l方程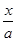 +
+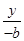 =1,即bx-ay-ab=0,由原点O到l的距离为
=1,即bx-ay-ab=0,由原点O到l的距离为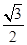 ,得
,得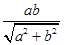 =
=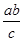 =
=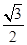 ,
,
又e=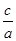 =
=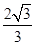 ,∴b=1,a=
,∴b=1,a=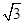 . 故所求双曲线方程为
. 故所求双曲线方程为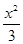 -y2=1.
-y2=1.
(2)显然直线m不与x轴垂直,设m方程为y=kx-1,
则点M、N坐标(x1,y1),(x2,y2)
是方程组y=kx-1,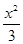 -y2=1的解,
-y2=1的解,
消去y,得(1-3k2)x2+6kx-6=0.①
依题意,1-3k2≠0,由根与系数关系,
知x1+x2=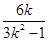 ,x1x2=
,x1x2=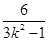
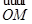 ·
·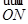 =(x1,y1)·(x2,y2)=x1x2+y1y2=x1x2+(kx1-1)(kx2-1)
=(x1,y1)·(x2,y2)=x1x2+y1y2=x1x2+(kx1-1)(kx2-1)
=(1+k2)x1x2-k(x1+x2)+1=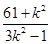 -
-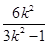 +1=
+1=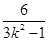 +1.
+1.
又∵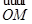 ·
·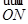 =-23,
=-23,
∴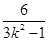 +1=-23,k=±
+1=-23,k=±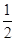 ,
,
当k=±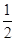 时,方程①有两个不相等的实数根,
时,方程①有两个不相等的实数根,
所以所求直线方程为y=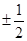 x-1.
x-1.

练习册系列答案
相关题目
 -
- =1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围.
=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围. -
- =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)