题目内容
抛物线y=-
x2的焦点坐标是
| 1 |
| 2 |
(0,-
)
| 1 |
| 2 |
(0,-
)
.| 1 |
| 2 |
分析:由抛物线的性质即可求得y=-
x2的焦点坐标.
| 1 |
| 2 |
解答:解:∵y=-
x2,
∴x2=-2y,
∴其焦点坐标为:(0,-
),
故答案为:(0,-
).
| 1 |
| 2 |
∴x2=-2y,
∴其焦点坐标为:(0,-
| 1 |
| 2 |
故答案为:(0,-
| 1 |
| 2 |
点评:本题考查抛物线的简单性质,掌握这些性质求得x2=-2y是解决问题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知P为抛物线y=
x2上的动点,点P在x轴上的射影为M,点A的坐标是(6,
),则|PA|+|PM|的最小值是( )
| 1 |
| 2 |
| 17 |
| 2 |
| A、8 | ||
B、
| ||
| C、10 | ||
D、
|
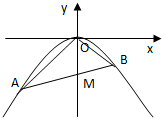 如图,抛物线
如图,抛物线