题目内容
在平面直角坐标系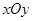 中,已知△ABC顶点
中,已知△ABC顶点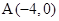 和
和 ,顶点B在椭圆
,顶点B在椭圆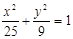 上,则
上,则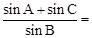 .
.
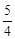
解析试题分析:根据题意,由椭圆的方程可得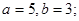
则其焦点坐标为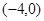 和
和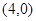 恰好是
恰好是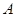 、
、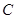 两点,则
两点,则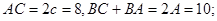
由正弦定理可得: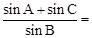
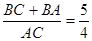 .
.
考点:椭圆的简单性质;正弦定理的应用.
点评:解题时,需注意特殊点的“巧合”,如本题中,通过计算可得,A、C就是焦点,进而结合椭圆
的性质,进行解题,其次要特别注意焦点三角形的有关性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
在平面直角坐标系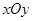 中,已知△ABC顶点
中,已知△ABC顶点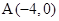 和
和 ,顶点B在椭圆
,顶点B在椭圆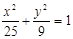 上,则
上,则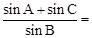 .
.
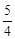
解析试题分析:根据题意,由椭圆的方程可得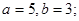
则其焦点坐标为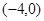 和
和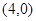 恰好是
恰好是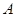 、
、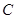 两点,则
两点,则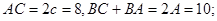
由正弦定理可得: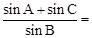
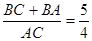 .
.
考点:椭圆的简单性质;正弦定理的应用.
点评:解题时,需注意特殊点的“巧合”,如本题中,通过计算可得,A、C就是焦点,进而结合椭圆
的性质,进行解题,其次要特别注意焦点三角形的有关性质.

 阅读快车系列答案
阅读快车系列答案