Question

（2012•东城区一模）如图，在边长为3的正方形ABCD中，点M在AD上，正方形ABCD以AD为轴逆时针旋转θ角(0≤θ≤

π

3

)到AB₁C₁D的位置，同时点M沿着AD从点A运动到点D，

MN1

=

DC1

，点Q在MN₁上，在运动过程中点Q始终满足|

QM

|=

1

cosθ

，记点Q在面ABCD上的射影为Q₀，则在运动过程中向量

BQ0

与

BM

夹角α的正切的最大值为

6

12

．

Answer 1

分析：该题先转化成平面几何问题，而运动过程中向量

BQ0

与

BM

夹角α即为∠MBQ₀，设BP=x，x∈[0，3]，然而根据tan∠MBQ₀=tan（∠MBP-∠Q₀BP）建立关于x的函数，最后利用基本不等式求出最值．

解答：解：由题意可知∠QMQ₀=θ，Q₀与AD距离始终是MQ₀=|

QM

|×cosθ=1
画出平面ABCD的图形

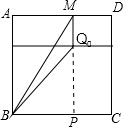
在运动过程中向量

BQ0

与

BM

夹角α即为∠MBQ₀，
由题意可设BP=x，x∈[0，3]
tan∠MBQ₀=tan（∠MBP-∠Q₀BP）=

3 x - 2 x

1+ 3 x × 2 x

=

x

x2+6

=

1

x+ 6 x

≤

1

2 6

=

6

12

当且仅当x=

6

时取等号
故答案为：

6

12

点评：本题主要考查了向量在几何中的应用，以及正切的差角公式，同时考查了利用基本不等式求最值，属于中档题．