题目内容
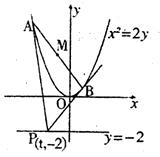
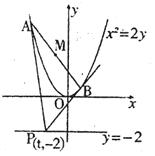
如图,已知抛物线![]() 上移动,过点P(t,-2)作抛物线的两条切线,切点分别为A,B,线段AB的中点为M。
上移动,过点P(t,-2)作抛物线的两条切线,切点分别为A,B,线段AB的中点为M。
(1)求点M的轨迹方程;
(2)求证直线AB过定点;
(3)求![]() 的值。
的值。
解:(1)由![]() 得
得![]()
∴![]()
则![]()
∵![]()
∴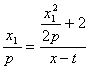 即
即![]() 同理
同理![]()
∴![]() 是方程
是方程![]() 的两根,
的两根,
由韦达定理![]()
设M(x,y)则![]()
![]()
![]()
∴M(x,y)的轨迹方程为![]()
(2)∵M为线段AB的中点
∴由①可知M![]() 可得AB的斜率
可得AB的斜率![]()
AB所在直线方程为![]()
(p>0)故直线过定点(0,2)
(3)由(2)知![]()

∴![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
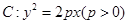 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.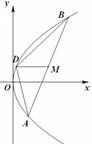
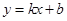 与抛物线C交于两点
与抛物线C交于两点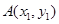 ,
,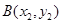 ,且
,且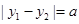 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到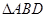 .
.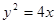 ,焦点为
,焦点为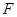 ,顶点为
,顶点为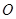 ,点
,点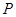 在抛物线上移动,
在抛物线上移动,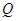 是
是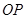 的中点,
的中点,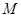 是
是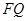 的中点,求点
的中点,求点