题目内容
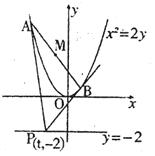
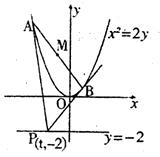
如图,已知抛物线![]() 上移动,过点P(t,-2)作抛物线的两条切线,切点分别为
上移动,过点P(t,-2)作抛物线的两条切线,切点分别为![]() ,线段AB的中点为M。
,线段AB的中点为M。
(1)分别用![]() ,
,![]() 表示切线PA,PB的斜率
表示切线PA,PB的斜率![]()
(2)证明![]() ,
,![]() 为方程
为方程![]() 的两根,并求线段AB长的最小值;
的两根,并求线段AB长的最小值;
(3)求直线AB与y轴的交点。
解:(1)由![]()
∵![]()
∴![]()
(2)∵![]()
∴结合(1)得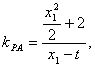
∴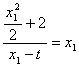
即![]()
∴![]()
![]()
∴![]()
![]()
![]()
∴当t=0时,![]()
(3)∵M为线段AB中点,
∴![]()
又![]()
∴M![]()
∵直线AB的斜率![]()
从而直线AB的方程![]()
即![]()
令x=0,由p>0得y=2,故直线AB与y轴交点为(0,2)

练习册系列答案
相关题目
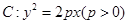 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.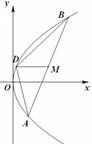
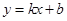 与抛物线C交于两点
与抛物线C交于两点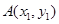 ,
,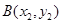 ,且
,且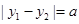 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到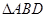 .
.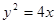 ,焦点为
,焦点为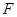 ,顶点为
,顶点为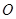 ,点
,点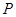 在抛物线上移动,
在抛物线上移动,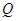 是
是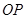 的中点,
的中点,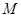 是
是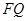 的中点,求点
的中点,求点