题目内容
设O为坐标原点，向量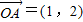
．将
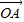绕着点O按逆时针方向旋转90°得到向量
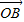，则2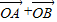
的坐标为 ．
【答案】分析：由已知中O为坐标原点，向量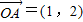
．我们易求出将
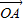逆时针方向旋转90°得到的向量
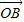的坐标，代入2
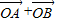，即可得到答案．
解答：解：设将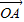
绕着点O按逆时针方向旋转90°得到向量
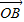=（x，y）（x＜0，y＞0）
∵向量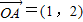
，
∴
•
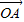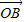=x+2y=0
|
|=|
|=
∴
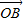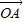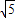
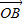=（-2，1），或
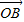=（2，-1）（舍去）
故2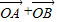
=2（1，2）+（-2，1）=（0，5）
故答案为：（0，5）
点评：本题考查的知识点是平面向量的加法坐标运算，根据已知计算出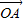
逆时针方向旋转90°得到的向量
的坐标是解答本题的关键．
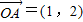．我们易求出将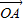逆时针方向旋转90°得到的向量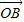的坐标，代入2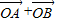，即可得到答案．解答：解：设将
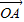绕着点O按逆时针方向旋转90°得到向量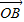=（x，y）（x＜0，y＞0）∵向量
，∴
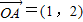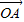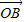•=x+2y=0|
|=||=∴
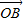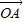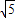
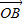=（-2，1），或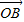=（2，-1）（舍去）故2
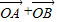=2（1，2）+（-2，1）=（0，5）故答案为：（0，5）
点评：本题考查的知识点是平面向量的加法坐标运算，根据已知计算出
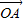逆时针方向旋转90°得到的向量的坐标是解答本题的关键． 
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
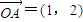．将
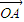绕着点O按逆时针方向旋转90°得到向量
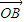，则2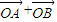
的坐标为 ．