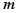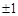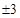题目内容
(满分12分) 已知函数 .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的单调增区间.
的单调增区间.
 .
.(1)若
 ,求
,求 的值;
的值;(2)求
 的单调增区间.
的单调增区间.(1) ;
;
(2) 的单调增区间为
的单调增区间为 .
.
 ;
;(2)
 的单调增区间为
的单调增区间为 .
.先通过降幂公式和三角恒等变换公式把f(x)转化成 .
.
(1)再根据 ,建立关于
,建立关于 的三角方程,求出
的三角方程,求出 的值.
的值.
(2)根据正弦函数的单调增区间求出f(x)的单调增区间.
 ………………… 1分
………………… 1分
 …………………… 3分
…………………… 3分
 …………………………. 5分
…………………………. 5分
(1) ;………….6分
;………….6分
 …………… 7分
…………… 7分
 …………… 8分
…………… 8分
(2) 单调递增,故
单调递增,故 ,………… 10分
,………… 10分
即 ,…………… 11分
,…………… 11分
从而 的单调增区间为
的单调增区间为 .…………… 12分
.…………… 12分
 .
.(1)再根据
 ,建立关于
,建立关于 的三角方程,求出
的三角方程,求出 的值.
的值.(2)根据正弦函数的单调增区间求出f(x)的单调增区间.
 ………………… 1分
………………… 1分 …………………… 3分
…………………… 3分 …………………………. 5分
…………………………. 5分(1)
 ;………….6分
;………….6分 …………… 7分
…………… 7分 …………… 8分
…………… 8分(2)
 单调递增,故
单调递增,故 ,………… 10分
,………… 10分即
 ,…………… 11分
,…………… 11分从而
 的单调增区间为
的单调增区间为 .…………… 12分
.…………… 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图像向左平移
的图像向左平移 个单位,再向上平移1个单位后所得图像对应的函数解析式是( )
个单位,再向上平移1个单位后所得图像对应的函数解析式是( )



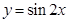 (
(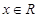 )的图象上所有点向左平行移动
)的图象上所有点向左平行移动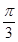 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的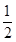 倍(纵坐标不变),得到的图象所表示的函数的解析式是( )
倍(纵坐标不变),得到的图象所表示的函数的解析式是( ) ,
, ,
, ,
,  ,
,  (
( ),对任意
),对任意 有
有 ,且
,且 ,那么
,那么 等于
等于 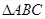 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为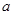 、
、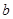 、
、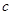 ,且
,且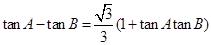 .
.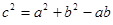 ,求角A、B、C大小;
,求角A、B、C大小;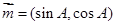 ,
,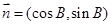 ,求
,求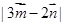 的取值范围.
的取值范围.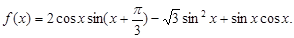
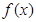 的最小正周期T;
的最小正周期T;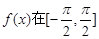 上的图象;
上的图象;
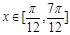 时,f (x)的反函数为
时,f (x)的反函数为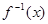 ,
,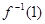 的值.
的值. 


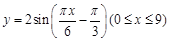 的最大值与最小值之和为( )
的最大值与最小值之和为( ) 
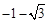
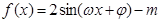 ,恒有
,恒有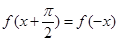 成立,且
成立,且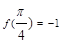 ,则实数
,则实数