题目内容
.(12分)设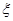 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量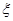 的期望
的期望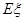 与方差
与方差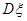 .
.
|
ξ |
-1 |
0 |
1 |
|
P |
|
1-2q[ |
q2 |
【答案】
|
ξ |
-1 |
0 |
1 |
|
P |
|
|
|
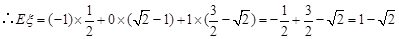
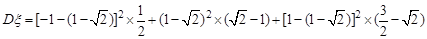
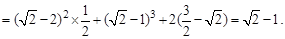
【解析】本题考查随机变量分布列的性质及应用、数学期望与方差的计算,属基本题
依题意,先应按分布列的性质,求出q的数值后,再计算出Eξ与Dξ.
因为 ,
,
那么可知q的值,进而代入期望和方差公式求解得到。
解:依题意,先应按分布列的性质,求出q的数值后,再计算出Eξ与Dξ.
由于离散型随机变量的分布列满足:
(1)pi≥0,i=1,2,3,…; (2)p1+p2+p3+…=1.
故 解得
解得 . …………6分
. …………6分
故ξ的分布列为
|
ξ |
-1 |
0 |
1 |
|
P |
|
|
|
 …………9分
…………9分

 …………12分
…………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本小题满分12分)设![]() 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量![]() 的期望
的期望![]() 与方差
与方差![]() .
.![]()
| ξ | -1 | 0 | 1 |
| P |
| 1-2q | q2 |
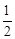


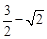
 是函数
是函数 的一个极值点.
的一个极值点. 与
与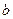 的关系式(用
的关系式(用 的单调区间;
的单调区间;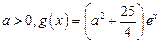 ,若存在
,若存在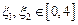 ,使得
,使得 成立,求
成立,求 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和 且
且 ,
, ,
, 成等比数列.(Ⅰ)证明
成等比数列.(Ⅰ)证明 ; (Ⅱ)求公差
; (Ⅱ)求公差 的值和数列
的值和数列 是函数
是函数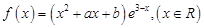 的一个极值点.
的一个极值点. 与
与 的关系式(用
的关系式(用 的单调区间;
的单调区间;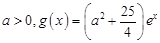 ,若存在
,若存在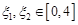 ,使得
,使得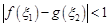 成立,求
成立,求