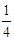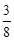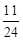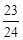题目内容
甲乙两人各有四张卡片,甲的卡片分别标有数字1、2、3、4,乙的卡片分别标有数字0、1、3、5.两人各自随机抽出一张,甲抽出卡片的数字记为a,乙抽出卡片的数字记为b,游戏规则是:若a和b的积为奇数,则甲赢,否则乙赢.
(1)请你运用概率计算说明这个游戏是否公平?
(2)若已知甲抽出的数字是奇数,求甲赢的概率.
(1)请你运用概率计算说明这个游戏是否公平?
(2)若已知甲抽出的数字是奇数,求甲赢的概率.
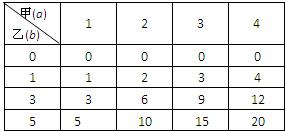
(1)将甲乙所得ab的所有可能结果列表如下:
 (2分)
(2分)
由表可知,ab的基本事件总数为16,其中“ab为奇数”(记为事件A)的结果有6种,“ab为偶数”(记为事件B)的结果有10种,(3分)
由此可得甲赢的概率为:P(A)=
=
;乙赢的概率为:P(B)=
=
;(5分)
∵P(A)<P(B),∴该游戏不公平.(6分)
(2)设“甲抽出的数字是奇数”为事件C,则C发生的概率为P(C)=
=
.(8分)
又由(1)知,甲赢的概率即事件A发生的概率,
∴P(CA)=P(A)=
(10分)
故由条件概率得此时甲赢的概率为P(A|C)=
=
=
.(12分)
 (2分)
(2分)由表可知,ab的基本事件总数为16,其中“ab为奇数”(记为事件A)的结果有6种,“ab为偶数”(记为事件B)的结果有10种,(3分)
由此可得甲赢的概率为:P(A)=
| 6 |
| 16 |
| 3 |
| 8 |
| 10 |
| 16 |
| 5 |
| 8 |
∵P(A)<P(B),∴该游戏不公平.(6分)
(2)设“甲抽出的数字是奇数”为事件C,则C发生的概率为P(C)=
| 2 |
| 4 |
| 1 |
| 2 |
又由(1)知,甲赢的概率即事件A发生的概率,
∴P(CA)=P(A)=
| 3 |
| 8 |
故由条件概率得此时甲赢的概率为P(A|C)=
| P(CA) |
| P(C) |
| ||
|
| 3 |
| 4 |

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
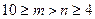 )中任选2个人当组长,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则(m,n)的可能值为 .
)中任选2个人当组长,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则(m,n)的可能值为 .