题目内容
二面角C-BD-A为直二面角,且DA⊥平面ABC,则△ABC的形状为( )A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
【答案】分析:根据“若两个相交平面都垂直于第三个平面,则它们的交线就垂直于第三个平面”可知:易证明CB⊥平面ABD,又因为AB?平面ABD,所以CB⊥AB,所以△ABC的形状为直角三角形.
解答: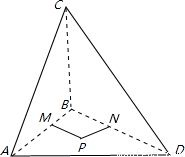 解:如图,
解:如图,
∵二面角C-BD-A为直二面角,
∴平面CBD⊥平面ABD
∵DA⊥平面ABC,DA?平面ABD,
∴平面ABC⊥平面ABD
在平面内任取一点P,过点P作PM⊥AB,垂足为M,过点P作PN⊥BD,垂足为N,
∵平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,PM?平面ABD,PM⊥AB,
∴PM⊥平面ABC
又∵CB?平面ABC,
∴PM⊥CB
同理:PN⊥CB
又∵PM∩PN=P,PM?平面ABD,PN?平面ABD,
∴CB⊥平面ABD
又∵AB?平面ABD
∴CB⊥AB,所以△ABC的形状为直角三角形
故选B
点评:本小题考查空间中的线面关系的基础知识,考查空间想象能力和思维能力.
解答:
 解:如图,
解:如图,∵二面角C-BD-A为直二面角,
∴平面CBD⊥平面ABD
∵DA⊥平面ABC,DA?平面ABD,
∴平面ABC⊥平面ABD
在平面内任取一点P,过点P作PM⊥AB,垂足为M,过点P作PN⊥BD,垂足为N,
∵平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,PM?平面ABD,PM⊥AB,
∴PM⊥平面ABC
又∵CB?平面ABC,
∴PM⊥CB
同理:PN⊥CB
又∵PM∩PN=P,PM?平面ABD,PN?平面ABD,
∴CB⊥平面ABD
又∵AB?平面ABD
∴CB⊥AB,所以△ABC的形状为直角三角形
故选B
点评:本小题考查空间中的线面关系的基础知识,考查空间想象能力和思维能力.

练习册系列答案
相关题目