题目内容
已知矩形ABCD，AB=2，BC=1，沿对角线BD将△ABC折起，使二面角C-BD-A为直二面角，则异面直线BD与AC所成角的余弦值为分析：画出图形，作AF⊥BD，CE⊥BD，AG∥EF，AG=EF，连接CG，则∠CAG就是异面直线BD与AC所成角，解三角形求出结果即可．
解答：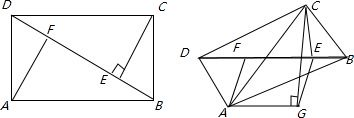
解：如图，作AF⊥BD，CE⊥BD，AG∥EF，AG=EF
连接CG，则∠CAG就是异面直线BD与AC所成角，
由题意，BD=
，AF=CE=
，
DF=BE=
，EF=
因为，二面角C-BD-A为直二面角，所以，△CEG和△AGC都是直角三角形，
CG=
，AC=
=
异面直线BD与AC所成角的余弦值：cos∠CAG=
=
故答案为：
解：如图，作AF⊥BD，CE⊥BD，AG∥EF，AG=EF连接CG，则∠CAG就是异面直线BD与AC所成角，
由题意，BD=
| 5 |
2
| ||
| 5 |
DF=BE=
| ||
| 5 |
3
| ||
| 5 |
因为，二面角C-BD-A为直二面角，所以，△CEG和△AGC都是直角三角形，
CG=
2
| ||
| 5 |
(
|
| ||
| 5 |
异面直线BD与AC所成角的余弦值：cos∠CAG=
| ||||
|
3
| ||
| 17 |
故答案为：
3
| ||
| 17 |
点评：本题考查异面直线及其所成的角，二面角及其度量，考查作图能力，计算能力，是基础题．
练习册系列答案
相关题目
已知矩形ABCD中，
如图所示，已知矩形ABCD中，AB=
的取值范围.