题目内容
.(本小题满分14分)
已知单调递增的等比数列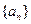 满足:
满足: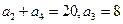 ;
;
(1)求数列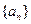 的通项公式;
的通项公式;
(2)若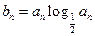 ,数列
,数列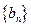 的前n项和为
的前n项和为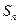 ,求
,求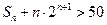 成立的正整数 n的最小值.
成立的正整数 n的最小值.
已知单调递增的等比数列
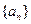 满足:
满足: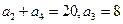 ;
;(1)求数列
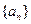 的通项公式;
的通项公式;(2)若
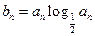 ,数列
,数列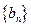 的前n项和为
的前n项和为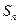 ,求
,求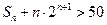 成立的正整数 n的最小值.
成立的正整数 n的最小值.【解】(1)设等比数列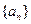 的首项为
的首项为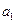 ,公比为q,
,公比为q,
依题意,有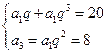 ,解之得
,解之得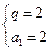 或
或 ; (…………4分)
; (…………4分)
又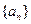 单调递增,∴
单调递增,∴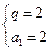 ,∴
,∴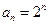 . (…………6分)
. (…………6分)
(2)依题意,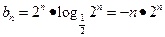 ,
, 
 (…………8分)
(…………8分)
∴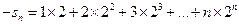 ①,
①,
∴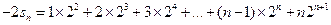 ②,
②,
∴①-②得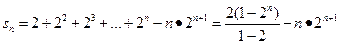 =
=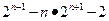 ;
;
 (……12分)
(……12分)
∴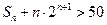 即为
即为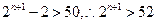 ,
,
∵当n≤4时,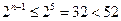 ;当n≥5时,
;当n≥5时,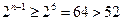 .
.
∴使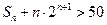 成立的正整数n的最小值为5. (…………14分)
成立的正整数n的最小值为5. (…………14分)
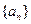 的首项为
的首项为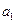 ,公比为q,
,公比为q,依题意,有
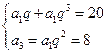 ,解之得
,解之得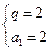 或
或 ; (…………4分)
; (…………4分)又
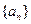 单调递增,∴
单调递增,∴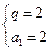 ,∴
,∴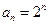 . (…………6分)
. (…………6分)(2)依题意,
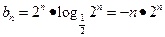 ,
, 
 (…………8分)
(…………8分)∴
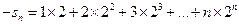 ①,
①,∴
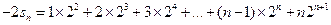 ②,
②,∴①-②得
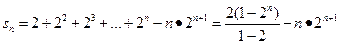 =
=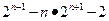 ;
; (……12分)
(……12分)∴
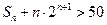 即为
即为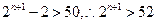 ,
,∵当n≤4时,
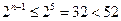 ;当n≥5时,
;当n≥5时,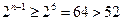 .
.∴使
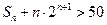 成立的正整数n的最小值为5. (…………14分)
成立的正整数n的最小值为5. (…………14分)略

练习册系列答案
相关题目
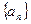 满足
满足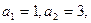 且
且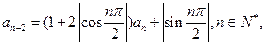
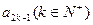 ;
;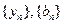 满足
满足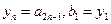 ,且
,且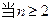 时
时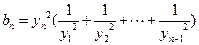 .
.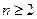 时,
时, 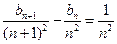 ;
;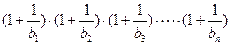 与4的大小关系.
与4的大小关系.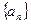 为等差数列,
为等差数列,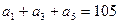 ,
,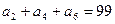 ,则
,则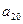 等于( )
等于( )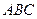 的三边
的三边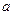 、
、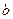 、
、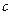 成等差且均为整数,公差为
成等差且均为整数,公差为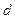 ,则下列命题不正确的是( )
,则下列命题不正确的是( )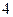 的倍数
的倍数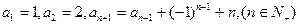
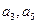 的值;
的值;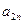 ;
;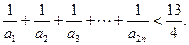
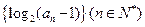 为等差数列,且
为等差数列,且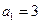 ,
,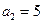 ,则
,则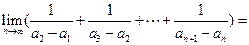 ___
___ _________.
_________.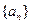 中,有
中,有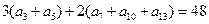 ,则此数列的前13项之和为( )
,则此数列的前13项之和为( )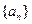 中,
中,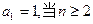 时,其前
时,其前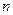 项和
项和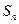 满足:
满足: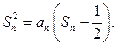
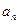 ;
;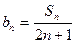 ,求数列
,求数列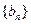 的前项和
的前项和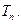
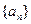 的前
的前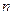 项和为
项和为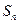 ,且
,且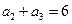 ,则
,则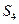 的值为
的值为