题目内容
设 ,函数
,函数 满足
满足 .
.
(Ⅰ)求 的单调递减区间;
的单调递减区间;
(Ⅱ)设锐角△ 的内角
的内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 , 求
, 求 的取值范围.
的取值范围.
(I) 的单调递减区间为:
的单调递减区间为: ;(II)
;(II) 取值范围为
取值范围为 .
.
解析试题分析:(I)首先将 降次得:
降次得: .由
.由 得:
得: ,
, .再将
.再将 化一得:
化一得: .结合正弦函数的单调区间便可得
.结合正弦函数的单调区间便可得 的单调递减区间.(II)从
的单调递减区间.(II)从 的特征来看,显然左边用余弦定理,右边用正弦定理,这样可得:
的特征来看,显然左边用余弦定理,右边用正弦定理,这样可得: ,
, ,
,  ,
, .又△
.又△ 是锐角三角形,所以
是锐角三角形,所以 ,这样根据角A的范围,便可确定
,这样根据角A的范围,便可确定 的取值范围.
的取值范围.
试题解析:(I) 2分
2分
由 得:
得: ,∴
,∴ 4分
4分
∴ 5分
5分
由 得:
得: ,
,
∴ 的单调递减区间为:
的单调递减区间为: 7分
7分
(II)∵ ,由余弦定理得:
,由余弦定理得: , 8分
, 8分
即 ,由正弦定理得:
,由正弦定理得: ,
, ,
,  ,∴
,∴ 11分
11分
∵△ 锐角三角形,∴
锐角三角形,∴ ,
, 12分
12分
∴ 的取值范围为
的取值范围为 . 13分
. 13分
考点:1、三角恒等变换;2、正弦定理和余弦定理;3、三角函数的性质.

练习册系列答案
相关题目
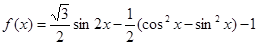
 的最小值和最小正周期;
的最小值和最小正周期; 的对边分别为a,b,c且
的对边分别为a,b,c且 =
= ,
, ,若向量
,若向量 共线,求
共线,求 的值.
的值.  sin
sin cos
cos ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 .
. ,S△ABC=2
,S△ABC=2 =
= ,求c的值.
,求c的值. -cos 2A=
-cos 2A= .
. ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积. 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 .设向量
.设向量 ,
, .
. ,
, ,求角
,求角 ,
,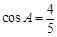 ,求
,求 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为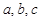 ,且
,且 ,
, ,求
,求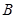 的取值范围.
的取值范围. 。
。 ,求
,求 的值。
的值。 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .
. 的大小;(Ⅱ)若
的大小;(Ⅱ)若 ,
, ;求
;求 .
. ,已知石塔的高度为
,已知石塔的高度为 .
.
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看 )最大,求山的高度
)最大,求山的高度