题目内容
某学生对函数f (x）=2xcosx进行研究后，得出如下四个结论：
①函数f(x)在[-π，0]上单调递增，在[0，π]上单调递减；
②存在常数M＞0，使|f(x)|≤M|x|对一切实数x均成立；
③点（
，0）是函数f（x）图象的一个对称中心；
④函数y=f（x）图象关于直线x=π对称；
其中正确的是（ ）。（把你认为正确命题的序号都填上）
①函数f(x)在[-π，0]上单调递增，在[0，π]上单调递减；
②存在常数M＞0，使|f(x)|≤M|x|对一切实数x均成立；
③点（
，0）是函数f（x）图象的一个对称中心； ④函数y=f（x）图象关于直线x=π对称；
其中正确的是（ ）。（把你认为正确命题的序号都填上）
②
练习册系列答案
中考解读考点精练系列答案
相关题目
上单调递增；
，0)是函数y＝f(x)图象的一个对称中心；
,
］上单调递增;②存在常数M＞0,使|f(x)|≤M|x|对一切实数x均成立;③函数f(x)在(0,π)上无最小值,但一定有最大值;④点(π,0)是函数y=f(x)图象的一个对称中心.其中正确的是
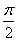，0）是函数y=f(x)图像的一个对称中心；