题目内容
已知函数f(x)=x3-3x的图象与直线y=a有相异三个公共点,则a的取值范围是 .
【答案】分析:先对函数f(x)求导,得出极值点及极值、单调区间,并求出其零点,根据以上结论画出图象,进而得到答案.
解答:解:∵函数f(x)=x3-3x,∴f′(x)=3x2-3=3(x+1)(x-1).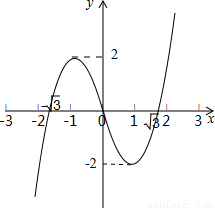
∴当x∈(-∞,-1)或(1,+∞)时,f′(x)>0,∴函数f(x)在区间(-∞,-1)或(1,+∞)上单调递增;
当x∈(-1,1)时,f′(x)<0,∴函数f(x)在区间(-1,1)上单调递减.
又f(x)=0,解得x=0,±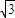 .
.
根据以上画出图象.
若函数f(x)=x3-3x的图象与直线y=a有相异三个公共点,则a必须满足f(x)min<y<f(x)max,∴-2<a<2.
所以a的取值范围是-2<a<2.
故答案 为-2<a<2.
点评:熟练利用导数得到极值及单调性是解题的关键.
解答:解:∵函数f(x)=x3-3x,∴f′(x)=3x2-3=3(x+1)(x-1).

∴当x∈(-∞,-1)或(1,+∞)时,f′(x)>0,∴函数f(x)在区间(-∞,-1)或(1,+∞)上单调递增;
当x∈(-1,1)时,f′(x)<0,∴函数f(x)在区间(-1,1)上单调递减.
又f(x)=0,解得x=0,±
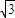 .
.根据以上画出图象.
若函数f(x)=x3-3x的图象与直线y=a有相异三个公共点,则a必须满足f(x)min<y<f(x)max,∴-2<a<2.
所以a的取值范围是-2<a<2.
故答案 为-2<a<2.
点评:熟练利用导数得到极值及单调性是解题的关键.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|